
9.如果实数满足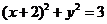 ,求
,求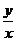 的最大值、2x-y的最小值
的最大值、2x-y的最小值
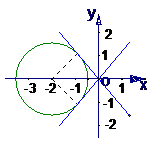 解:(1)问题可转化为求圆
解:(1)问题可转化为求圆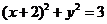 上一点到原点连线的斜率
上一点到原点连线的斜率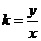 的最大值, 由图形性质可知, 由原点向圆
的最大值, 由图形性质可知, 由原点向圆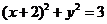 作切线,其中切线斜率的最大值即为
作切线,其中切线斜率的最大值即为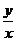 的最大值
的最大值
设过原点的直线为y=kx,即kx-y=0,
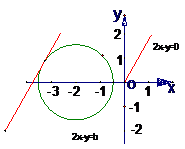 由
由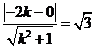 ,解得
,解得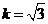 或
或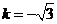
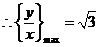

(2) x,y满足
x,y满足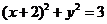 ,
,
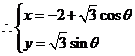
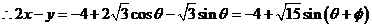
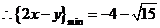

[典型考例]
[问题1]直线的方程与平行、垂直条件
P91 例1
例2.若直线mx+y+2=0与线段AB有交点,其中A(-2, 3),B(3,2),求实数m的取值范围。
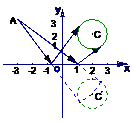 例3.自点A(-3,3)发出的光线
例3.自点A(-3,3)发出的光线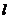 射到x轴上,被x轴反射,其反射光线所在的直线与圆
射到x轴上,被x轴反射,其反射光线所在的直线与圆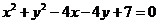 相切,求光线
相切,求光线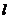 所在的直线方程
所在的直线方程
解:由已知可得圆C: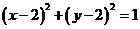 关于x轴对称的圆C‘的方程为
关于x轴对称的圆C‘的方程为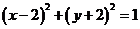 ,其圆心C‘(2,-2),则
,其圆心C‘(2,-2),则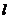 与圆C’相切,
与圆C’相切,
设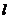 : y-3=k(x+3),
: y-3=k(x+3),
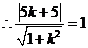 ,
,
整理得12k2+
25k+12=0, 解得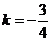 或
或 ,
,
所以所求直线方程为y-3=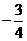 (x+3)或 y-3=
(x+3)或 y-3=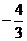 (x+3),
(x+3),
即 3x+4y-3=0或4x+3y+3=0
[问题2]圆的方程
例4.P92 例2
例5.(04年湖南文理科试题)如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点。(I)设点P分有向线段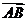 所成的比为
所成的比为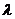 ,证明:
,证明:
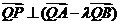 (II)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
(II)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
解:(Ⅰ)依题意,可设直线AB的方程为 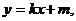 代入抛物线方程
代入抛物线方程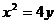 得
得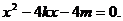 ①
①
设A、B两点的坐标分别是 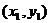 、
、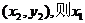 、x2是方程①的两根.
、x2是方程①的两根.
所以 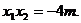
由点P(0,m)分有向线段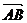 所成的比为
所成的比为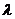 ,得
,得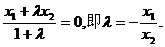
又点Q是点P关于原点的对称点,故点Q的坐标是(0,-m),从而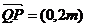 .
.
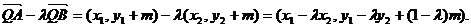
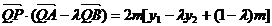
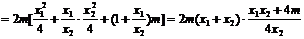
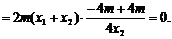
所以 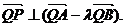
(Ⅱ)由 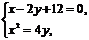 得点A、B的坐标分别是(6,9)、(-4,4).
得点A、B的坐标分别是(6,9)、(-4,4).
由 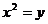 得
得 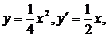 所以抛物线
所以抛物线 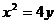 在点A处切线的斜率为
在点A处切线的斜率为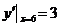
设圆C的方程是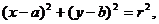 则
则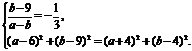
解之得
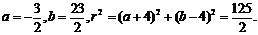
所以圆C的方程是
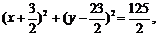 即
即 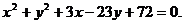
例6.一个圆和已知圆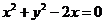 外切,并与直线
外切,并与直线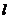 :
: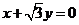 相切于点M(
相切于点M(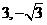 ),求该圆的方程
),求该圆的方程
已知圆方程化为: 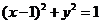 ,其圆心P(1,0),半径为1
,其圆心P(1,0),半径为1
设所求圆的圆心为C(a,b), 则半径为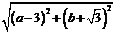 ,
,
因为两圆外切,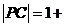
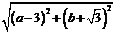 ,从而
,从而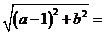 1+
1+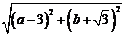 (1)
(1)
又所求圆与直线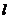 :
: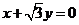 相切于M(
相切于M(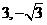 ),
),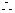 直线
直线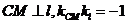 ,于是
,于是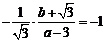 ,
,
即 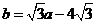 (2) 将(2)代入(1)化简,得a2-4a=0,
(2) 将(2)代入(1)化简,得a2-4a=0, 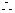 a=0或a=4
a=0或a=4
 当a=0时,
当a=0时,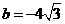 ,所求圆方程为
,所求圆方程为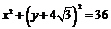
当a=4时,b=0,所求圆方程为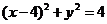

[问题3]直线与圆的位置关系
例7.P96T8 例8. P96 T9
[问题3]综合与提高
例9: 例3. 2.(广东卷)在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图5所示).将矩形折叠,使A点落在线段DC上.
(Ⅰ)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.
例10. 23.如图,过圆O:x2+y2=4与y轴正半轴交点A作此圆的切线,M为上任一点,过M作圆O的另一条切线,切点为Q,求△MAQ垂心P的轨迹方程。
[课后训练]
6. (辽宁卷)若直线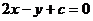 按向量
按向量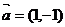 平移后与圆
平移后与圆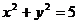 相切,则c的值为( A )
相切,则c的值为( A )
A.8或-2 B.6或-4 C.4或-6 D.2或-8
7(北京卷)从原点向圆 x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为 (B )
(A)π (B)2π (C)4π (D)6π
8(湖南卷)设直线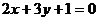 和圆
和圆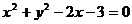 相交于点A、B,则弦AB的垂直平分线方程是
相交于点A、B,则弦AB的垂直平分线方程是 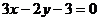 .
.
5.(重庆卷)过坐标原点且与x2+y2 +
4x+2y+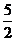 =0相切的直线的方程为
=0相切的直线的方程为
(A)y=-3x或y=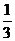 x (B) y=-3x或y=-
x (B) y=-3x或y=-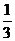 x (C)y=3x或y=-
x (C)y=3x或y=-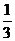 x (B) y=3x或y=
x (B) y=3x或y=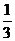 x
x
解析:过坐标原点的直线为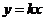 ,与圆
,与圆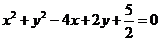 相切,则圆心(2,-1)到直线方程的距离等于半径
相切,则圆心(2,-1)到直线方程的距离等于半径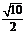 ,则
,则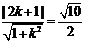 ,解得
,解得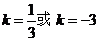 ,∴ 切线方程为
,∴ 切线方程为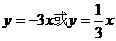 ,选A.
,选A.
3.(全国卷I)从圆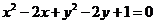 外一点
外一点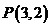 向这个圆作两条切线,则两切线夹角的余弦值为
A.
向这个圆作两条切线,则两切线夹角的余弦值为
A.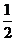 B.
B.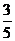 C.
C.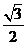 D.
D.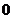
解析:圆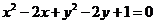 的圆心为M(1,1),半径为1,从外一点
的圆心为M(1,1),半径为1,从外一点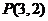 向这个圆作两条切线,则点P到圆心M的距离等于
向这个圆作两条切线,则点P到圆心M的距离等于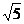 ,每条切线与PM的夹角的正切值等于
,每条切线与PM的夹角的正切值等于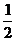 ,所以两切线夹角的正切值为
,所以两切线夹角的正切值为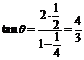 ,该角的余弦值等于
,该角的余弦值等于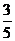 ,选B.
,选B.
2.(江苏卷)圆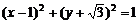 的切线方程中有一个是
的切线方程中有一个是
(A)x-y=0 (B)x+y=0 (C)x=0 (D)y=0
[正确解答]直线ax+by=0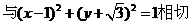 ,则
,则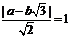 ,由排除法,
,由排除法,
选C,本题也可数形结合,画出他们的图象自然会选C,用图象法解最省事。
[解后反思]直线与圆相切可以有两种方式转化(1)几何条件:圆心到直线的距离等于半径(2)代数条件:直线与圆的方程组成方程组有唯一解,从而转化成判别式等于零来解.
1.(湖南卷)若圆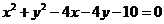 上至少有三个不同点到直线
上至少有三个不同点到直线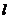 :
: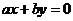 的距离为
的距离为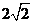 ,则直线
,则直线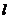 的倾斜角的取值范围是 ( )A.[
的倾斜角的取值范围是 ( )A.[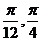 ] B.[
] B.[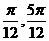 ] C.[
] C.[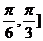 D.
D.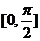
解析:圆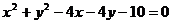 整理为
整理为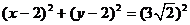 ,∴圆心坐标为(2,2),半径为3
,∴圆心坐标为(2,2),半径为3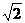 ,要求圆上至少有三个不同的点到直线
,要求圆上至少有三个不同的点到直线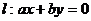 的距离为
的距离为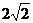 ,则圆心到直线的距离应小于等于
,则圆心到直线的距离应小于等于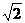 , ∴
, ∴ 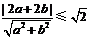 ,∴
,∴ 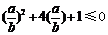 ,∴
,∴ 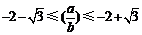 ,
,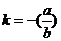 ,
,
∴ 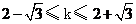 ,直线
,直线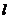 的倾斜角的取值范围是
的倾斜角的取值范围是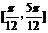 ,选B.
,选B.
6.设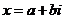 ,
,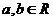 ,代入原方程整理得
,代入原方程整理得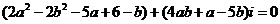
有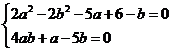 ,解得
,解得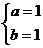 或
或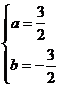 ,所以
,所以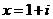 或
或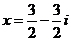 .
.
5.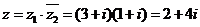 ,它对应的点位于第一象限.
,它对应的点位于第一象限.
6.在复数集C内,方程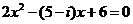 的解为
.
的解为
.
答案:1.4 2。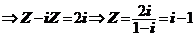 3。3
4。
3。3
4。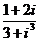 =
=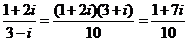
5.复数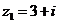 ,
,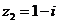 ,则
,则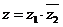 在复平面内的对应点位于第 象限.
在复平面内的对应点位于第 象限.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com