
11.已知圆C: x2+y2-2x+4y-4=0,是否存在斜率为1的直线L,使以L被圆C截得弦AB为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由
解:设直线L的斜率为1,且L的方程为y=x+b,则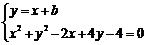 消元得方程2x2+(2b+2)x+b2+4b-4=0,设此方程两根为x1,x2,则x1+x2=-(b+1),y1+y2= x1+x2+2b=b-1,则AB中点为
消元得方程2x2+(2b+2)x+b2+4b-4=0,设此方程两根为x1,x2,则x1+x2=-(b+1),y1+y2= x1+x2+2b=b-1,则AB中点为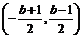 ,又弦长为
,又弦长为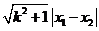 =
= ,由题意可列式
,由题意可列式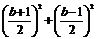 =
=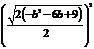 解得b=1或b=-9,经检验b=-9不合题意.所以所求直线方程为y=x+1
解得b=1或b=-9,经检验b=-9不合题意.所以所求直线方程为y=x+1
考点透析10答案:
考点小测答案:
课后练习答案:
10、当0<a<2时,直线L1:ax-2y-2a+4=0与L2:2x+a2y-2a2-4=0和坐标轴成一个四边形,要使围成的四边形面积最小,a应取何值?
9.(江苏卷) 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得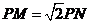 试建立适当的坐标系,并求动点 P的轨迹方程.
试建立适当的坐标系,并求动点 P的轨迹方程.
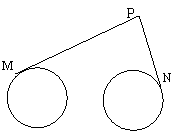 解:如图,以直线
解:如图,以直线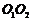 为
为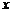 轴,线段
轴,线段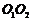 的垂直平分线为
的垂直平分线为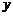 轴,建立平面直角坐标系,则两圆心分别为
轴,建立平面直角坐标系,则两圆心分别为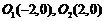 .设
.设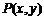 ,则
,则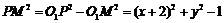 ,同理
,同理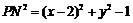 .
.
∵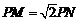 ,
,
∴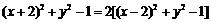 ,
,
即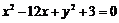 ,即
,即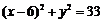 .这就是动点
.这就是动点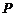 的轨迹方程.
的轨迹方程.
8.(上海卷)已知两条直线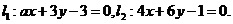 若
若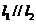 ,则
,则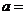 ____.
____.
解:两条直线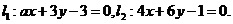 若
若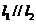 ,
,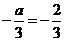 ,则
,则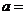 2.
2.
7.(湖北卷)若直线y=kx+2与圆(x-2)2+(y-3)2=1有两个不同的交点,则k 的取值范围是 .
解:由直线y=kx+2与圆(x-2)2+(y-3)2=1有两个不同的交点可得直线与圆的位置关系是相交,故圆心到直线的距离小于圆的半径,即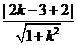 <1,解得kÎ(0,
<1,解得kÎ(0,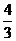 )
)
6.(湖北卷)已知直线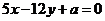 与圆
与圆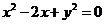 相切,则
相切,则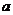 的值为
。
的值为
。
解:圆的方程可化为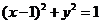 ,所以圆心坐标为(1,0),半径为1,由已知可得
,所以圆心坐标为(1,0),半径为1,由已知可得
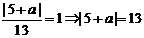 ,所以
,所以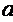 的值为-18或8。
的值为-18或8。
5. (全国卷I)已知直线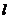 过点
过点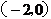 ,当直线
,当直线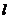 与圆
与圆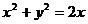 有两个交点时,其斜率k的取值范围是(B)
有两个交点时,其斜率k的取值范围是(B)
(A) (B)
(B)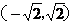 (C)
(C)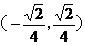 (D)
(D)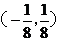
3.(江西卷) “a=b”是“直线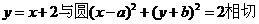 ”的 (A )
”的 (A )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件
4 (重庆卷)圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程为 (A )
(A) (x-2)2+y2=5; (B) x2+(y-2)2=5; (C) (x+2)2+(y+2)2=5; (D) x2+(y+2)2=5。
2.(陕西卷)设直线过点(0,a),其斜率为1, 且与圆x2+y2=2相切,则a 的值为( )
A.± B.±2 B.±2 D.±4
解析:设直线过点(0,a),其斜率为1, 且与圆x2+y2=2相切,设直线方程为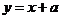 ,圆心(0,0)道直线的距离等于半径
,圆心(0,0)道直线的距离等于半径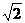 ,∴
,∴ 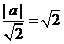 ,∴ a 的值±2,选B.
,∴ a 的值±2,选B.
1.(安徽卷)直线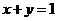 与圆
与圆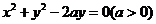 没有公共点,则
没有公共点,则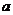 的取值范围是
的取值范围是
A.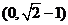 B.
B.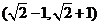 C.
C.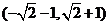 D.
D.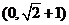
解:由圆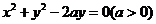 的圆心
的圆心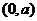 到直线
到直线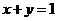 大于
大于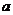 ,且
,且 ,选A。
,选A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com