
7.给出下列关于互不相同的直线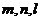 和平面
和平面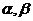 的四个命题:
的四个命题:
① 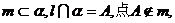 则
则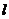 与m不共面;
与m不共面;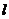 、m是异面直线,
、m是异面直线,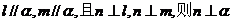 ;
;
② 若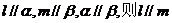 ;若
;若 ,则
,则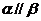
其中为假命题的是 (C)(A)① (B)② (C)③ (D)④
6. 在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是( )
(A)BC//平面PDF (B)DF⊥平面PA E (C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
5.(上海卷)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .
4.(上海卷)若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 ( )
(A)充分非必要条件;(B)必要非充分条件;(C)充要条件;(D)非充分非必要条件
3.(湖北卷)关于直线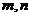 与平面
与平面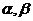 ,有以下四个命题:①若
,有以下四个命题:①若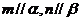 且
且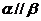 ,则
,则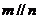 ;②若
;②若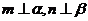 且
且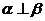 ,则
,则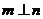 ;③若
;③若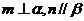 且
且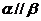 ,则
,则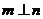 ;④若
;④若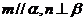 且
且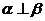 ,则
,则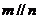 ;其中真命题的序号是 A.①② B.③④ C.①④ D.②③
;其中真命题的序号是 A.①② B.③④ C.①④ D.②③
2.(北京卷)平面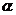 的斜线
的斜线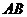 交
交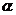 于点
于点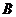 ,过定点
,过定点 的动直线
的动直线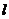 与
与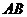 垂直,且交
垂直,且交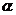 于点
于点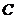 ,则动点
,则动点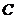 的轨迹是 (A)一条直线 (B)一个圆(C)一个椭圆(D)双曲线的一支
的轨迹是 (A)一条直线 (B)一个圆(C)一个椭圆(D)双曲线的一支
1. 已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面.给出下列的四个命题:
①若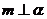 ,
,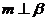 ,则
,则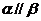 ;②若
;②若 ,
,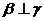 ,则
,则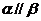 ;③若
;③若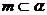 ,
,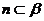 ,
,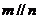 ,则
,则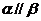 ;
;
④若m、n是异面直线,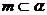 ,
,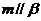 ,
,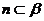 ,
,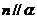 ,则
,则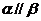 ,其中真命题是
,其中真命题是
A.①和② B.①和③ C.③和④ D.①和④
10.(山东卷)已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4.。(Ⅰ)求椭圆的方程;
(Ⅱ)直线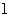 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.(15班)
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.(15班)
解:设椭圆方程为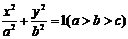
(Ⅰ)由已知得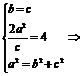
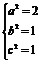 ∴所求椭圆方程为
∴所求椭圆方程为 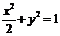 .
.
(Ⅱ)解法一:由题意知直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为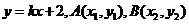
由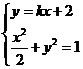 ,消去y得关于x的方程:
,消去y得关于x的方程: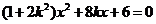
由直线 与椭圆相交于A、B两点,
与椭圆相交于A、B两点,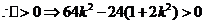 解得
解得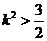
又由韦达定理得
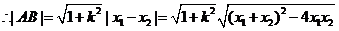
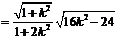
原点 到直线
到直线 的距离
的距离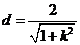
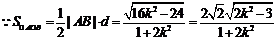 .
.
解法1:对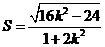 两边平方整理得:
两边平方整理得: (*)
(*)
∵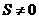 ,
,
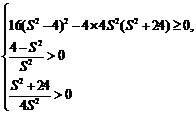 整理得:
整理得: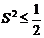
又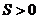 ,
, 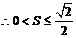 从而
从而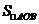 的最大值为
的最大值为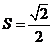 ,
,
此时代入方程(*)得 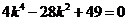
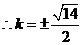
所以,所求直线方程为: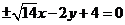 .
.
解法2:令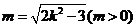 , 则
, 则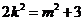
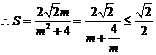
当且仅当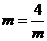 即
即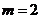 时,
时, 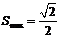 此时
此时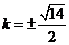 .
.
所以,所求直线方程为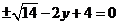
解法二:由题意知直线l的斜率存在且不为零.设直线l的方程为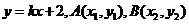 ,则直线l与x轴的交点
,则直线l与x轴的交点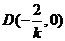 ,
,
由解法一知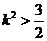 且
且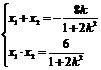 ,
,
解法1: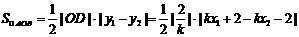 =
=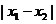
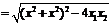
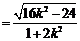
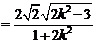 .
.
下同解法一.
解法2: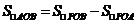
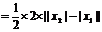
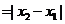 =
=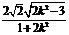
下同解法一.
9.(全国II)已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且=λ(λ>0).过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明·为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.(15班)
解:(Ⅰ)由已知条件,得F(0,1),λ>0.设A(x1,y1),B(x2,y2).由=λ,
即得 (-x1,1-y)=λ(x2,y2-1),
将①式两边平方并把y1=x12,y2=x22代入得 y1=λ2y2 ③
解②、③式得y1=λ,y2=,且有x1x2=-λx22=-4λy2=-4,
抛物线方程为y=x2,求导得y′=x.
所以过抛物线上A、B两点的切线方程分别是
y=x1(x-x1)+y1,y=x2(x-x2)+y2,即y=x1x-x12,y=x2x-x22.
解出两条切线的交点M的坐标为(,)=(,-1). ……4分
所以·=(,-2)·(x2-x1,y2-y1)=(x22-x12)-2(x22-x12)=0
所以·为定值,其值为0. ……7分
(Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S=|AB||FM|.
|FM|===
==+.
因为|AF|、|BF|分别等于A、B到抛物线准线y=-1的距离,所以
|AB|=|AF|+|BF|=y1+y2+2=λ++2=(+)2.
于是 S=|AB||FM|=(+)3,
由+≥2知S≥4,且当λ=1时,S取得最小值4.
由= +得M的坐标为(x,y), 由x0,y0满足C的方程,得点M的轨迹方程为:
+ =1 (x>1,y>2)
(Ⅱ)| 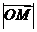 2= x2+y2, y2= =4+ ,
2= x2+y2, y2= =4+ ,
∴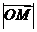 2= x2-1++5≥4+5=9.且当x2-1= ,即x=>1时,上式取等号.
2= x2-1++5≥4+5=9.且当x2-1= ,即x=>1时,上式取等号.
故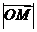 的最小值为3.
的最小值为3.
8.(上海卷)在平面直角坐标系 O
O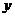 中,直线
中,直线 与抛物线
与抛物线 =2
=2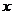 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线 过点T(3,0),那么
过点T(3,0),那么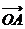
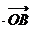 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.(15班)
[解](1)设过点T(3,0)的直线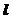 交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
当直线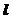 的钭率不存在时,直线
的钭率不存在时,直线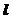 的方程为x=3,此时,直线
的方程为x=3,此时,直线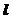 与抛物线相交于点A(3,
与抛物线相交于点A(3,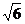 )、B(3,-
)、B(3,-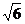 ).
∴
).
∴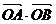 =3;
=3;
当直线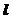 的钭率存在时,设直线
的钭率存在时,设直线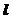 的方程为
的方程为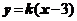 ,其中
,其中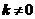 ,
,
由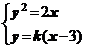 得
得 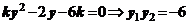
又 ∵ 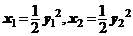 ,
,
∴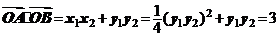 ,
,
综上所述,命题“如果直线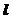 过点T(3,0),那么
过点T(3,0),那么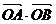 =3”是真命题;
=3”是真命题;
(2)逆命题是:设直线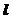 交抛物线y2=2x于A、B两点,如果
交抛物线y2=2x于A、B两点,如果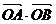 =3,那么该直线过点T(3,0).该命题是假命题.
=3,那么该直线过点T(3,0).该命题是假命题.
例如:取抛物线上的点A(2,2),B(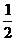 ,1),此时
,1),此时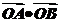 =3,直线AB的方程为:
=3,直线AB的方程为: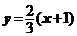 ,而T(3,0)不在直线AB上;
,而T(3,0)不在直线AB上;
说明:由抛物线y2=2x上的点A (x1,y1)、B (x2,y2) 满足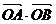 =3,可得y1y2=-6,
=3,可得y1y2=-6,
或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com