
2. (06天津)某公司一年购买某种货物400吨,每次都购买
(06天津)某公司一年购买某种货物400吨,每次都购买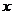 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为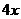 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则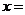 20 吨.
20 吨.
1.(06陕西)为确保信息安全,信息需加密传输,发送方由明文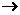 密文(加密),接收方由密文
密文(加密),接收方由密文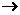 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文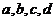 对应密文
对应密文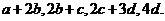 例如,明文
例如,明文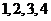 对应密文
对应密文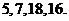 当接收方收到密文
当接收方收到密文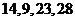 时,则解密得到的明文为(C)
时,则解密得到的明文为(C)
(A)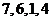 (B)
(B)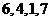 (C)
(C)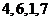 (D)
(D)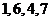
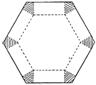
7.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为( )
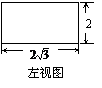
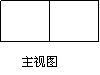
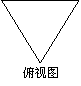
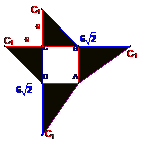 (A)2,2
(A)2,2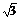 (B)
2
(B)
2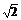 ,2
(C)4,2 (D)2,4
,2
(C)4,2 (D)2,4
[典型考例]
例1如图为一几何体的展开图 (I) 需要多少个这样的几何体才能拼成一
个棱长为6cm的正方体ABCD-A1B1C1D1,请画出其示意图(需在示意
图中分别表示出这种几何体);(Ⅱ)设正方体ABCD-A1B1C1D1的棱CC1
的中点为E,试求:异面直线EB与AB1所成角的余弦值及平面AB1E与
平面ABC所成二面角(锐角)的正切值.
例2.已知正四棱柱ABCD-A1B1C1D1.AB=1,AA1=2,点E为CC1中点,点P为BD1中点.
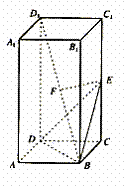 (1)证明EF为BD1与CC1的公垂线;
(1)证明EF为BD1与CC1的公垂线;
(2)求点D1到面BDE的距离.
(1)证法一:取BD中点M.连结MC,FM .
∵F为BD1中点 , ∴FM∥D1D且FM=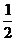 D1D .
D1D .
又EC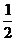 CC1且EC⊥MC ,∴四边形EFMC是矩形
CC1且EC⊥MC ,∴四边形EFMC是矩形
∴EF⊥CC1. 又CM⊥面DBD1 .∴EF⊥面DBD1 .
∵BD1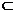 面DBD1 . ∴EF⊥BD1
. 故EF为BD1
与CC1的公垂线.
面DBD1 . ∴EF⊥BD1
. 故EF为BD1
与CC1的公垂线.
证法二:建立如图的坐标系,得
B(0,1,0),D1(1,0,2),F(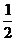 ,
,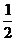 ,1),C1(0,0,2),E(0,0,1).
,1),C1(0,0,2),E(0,0,1).
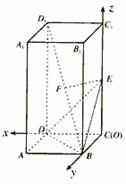
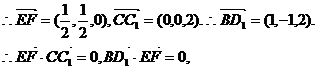
即EF⊥CC1,EF⊥BD1 . 故EF是为BD1 与CC1的公垂线.
(Ⅱ)解:连结ED1,有VE-DBD1=VD1-DBE .
由(Ⅰ)知EF⊥面DBD1 ,设点D1到面BDE的距离为d.
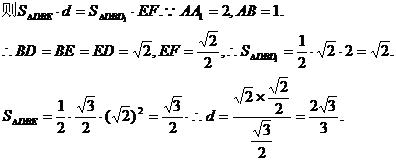
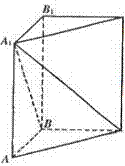 故点D1到平面DBE的距离为
故点D1到平面DBE的距离为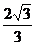 .
.
例3.(2006上海文)在三棱柱 ABC-A1B1C1 中,∠ABC=90°,AB=BC=1。
(1)求异面直线 B1C1 与 AC所成角的大小;
(2)若直线 A1C与平面 ABC所成角为 45°,求三棱锥 A1-ABC的体积。
 例4.(2006上海理)在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60
例4.(2006上海理)在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60 ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60 .
.
(1)求四棱锥P-ABCD的体积;
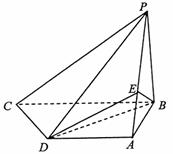
例5.如图,四棱锥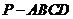 中,
中, ⊥底面
⊥底面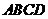 ,
,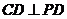 .底面
.底面 为直角梯形,
为直角梯形,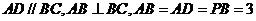 .点
.点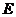 在棱
在棱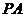 上,且
上,且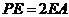 .(1)求证:平面
.(1)求证:平面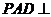 平面
平面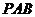 ;(2)求证:
;(2)求证: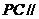 平面
平面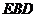 .
.
6.设地球半径为R,在北纬60°的纬度圈上有M,N两点,它们的纬度圈的弧线等于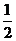
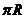 ,则这两点间的球面距离是
,则这两点间的球面距离是
A. B.
B.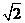
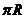 C.
C.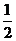
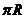 D.
D.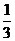
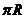
5.全国卷I)已知正四棱锥的体积为12,底面对角线的长为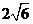 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。
[解析]正四棱锥的体积为12,底面对角线的长为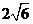 ,底面边长为2
,底面边长为2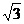 ,底面积为12,所以正四棱锥的高为3,则侧面与底面所成的二面角的正切tanα=
,底面积为12,所以正四棱锥的高为3,则侧面与底面所成的二面角的正切tanα=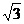 , ∴ 二面角等于
, ∴ 二面角等于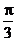 。
。
4.(天津卷)如图,在正三棱柱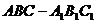 中,
中,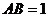 .
.
若二面角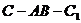 的大小为
的大小为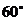 ,则点
,则点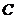 到平面
到平面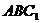 的距
的距
离为______________.
解析:过C作CD⊥AB,D为垂足,连接C1D,则C1D⊥AB,∠C1DC=60°,CD=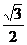 ,则C1D=
,则C1D=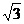 ,CC1=
,CC1=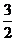 ,在△CC1D中,过C作CE⊥C1D,则CE为点C到平面
,在△CC1D中,过C作CE⊥C1D,则CE为点C到平面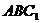 的距离,CM=
的距离,CM=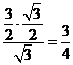 ,所以点C到平面
,所以点C到平面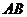 C1的距离为
C1的距离为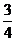 .
.
4.正方体的内切球与其外接球的体积之比为 (A) 1∶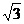 (B)1∶3
(C)1∶3
(B)1∶3
(C)1∶3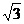 (D)1∶9
(D)1∶9
解:设正方体的棱长为a,则它的内切球的半径为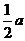 ,它的外接球的半径为
,它的外接球的半径为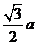 ,故所求的比为1∶3
,故所求的比为1∶3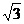 ,选C
,选C
3.(广东卷)棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______.
解: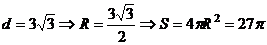
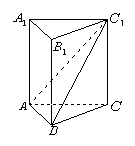
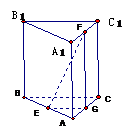
2.(浙江卷)如图,正三棱柱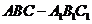 的各棱长都2,E,F分别是
的各棱长都2,E,F分别是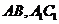 的中点,则EF的长是
的中点,则EF的长是
 (A)2 (B)
(A)2 (B)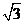 (C)
(C) 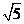 (D)
(D)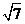
解析:如图所示,取AC的中点G,连EG,FG,则易得
EG=2,EG=1,故EF=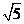 ,选C
,选C
1.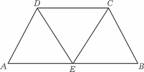 (山东卷)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为
(山东卷)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为
(A)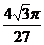 (B)
(B)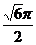 (C)
(C)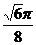 (D)
(D)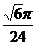
解:易证所得三棱锥为正四面体,它的棱长为1,故外接球半径为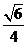 ,外接球的体积为
,外接球的体积为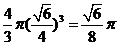 ,选C
,选C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com