
1.2 漏洞隐蔽性:数学解题是考生借助特定“数学语言”进行数学思维的过程,在这个过程中考生的数学知识结构和数学思维习惯有着决定性的作用。个体思维的跳跃性是产生思维漏洞的根本原因,这种思维漏洞一旦产生,考生是很难发现的,考生本人还处我感觉很好。这是思维跳跃度大和平时解题不写过程的考生的共同特点。(是聪明人犯的愚蠢的错误)
5、规律探究型问题,通常需要研究简化形式但保持本质的特殊情形,从条件出发,通过观察、试验、归纳、类比、猜测、联想来探路,解题过程中创新成分比较高.
4、规律探究型问题,通常需要研究简化形式但保持本质的特殊情形,从条件出发,通过观察、试验、归纳、类比、猜测、联想来探路,解题过程中创新成分比较高.
3、条件重组型问题,通常假定题中的数学对象存在(或结论成立)或暂且认可其中的一部分的结论,然后在这个前提下进行逻辑推理,若由此导出矛盾,则否定假设;否则,给出肯定结论.其中反证法在解题中起着重要的作用.
2、 结论探索型问题,先探索结论而后去论证结论.在探索过程中常可先从特殊情形入手,通过观察、分析、归纳、判断来作一番猜测,得出结论,再就一般情形去认证结论.
这类问题的基本特征是:未给出问题的结论,需要由特殊情况入手,猜想、证明一般结论.解决这类问题的基本策略是:通常需要研究简化形式但保持本质的特殊情形,从条件出发,通过观察、试验、归纳、类比、猜测、联想来探路,解题过程中创新成分比较高.
例8:(06年上海春)已知数列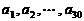 ,其中
,其中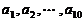 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为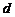 的等差数列;
的等差数列;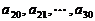 是公差为
是公差为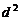 的等差数列(
的等差数列(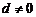 ).
).
(1)若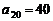 ,求
,求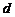 ;(2)试写出
;(2)试写出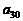 关于
关于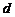 的关系式,并求
的关系式,并求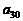 的取值范围;
的取值范围;
(3)续写已知数列,使得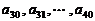 是公差为
是公差为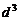 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
思路分析: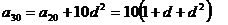 ,
,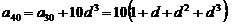 ,
,
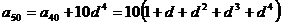 ,由此得到
,由此得到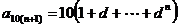
解:(1)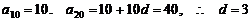 .
.
(2)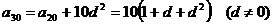 ,
,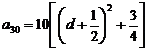 ,
,
当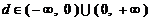 时,
时,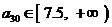 .
.
(3)所给数列可推广为无穷数列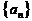 ,其中
,其中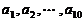 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当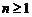 时,数列
时,数列 是公差为
是公差为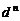 的等差数列.
的等差数列.
研究的问题可以是:试写出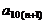 关于
关于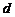 的关系式,并求
的关系式,并求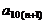 的取值范围
的取值范围
研究的结论可以是:由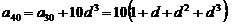 ,
,
依次类推可得 
当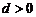 时,
时,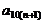 的取值范围为
的取值范围为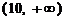 等.
等.
专题小结
1、 条件探索型题目,其结论明确,需要完备使得结论成立的充分条件,可变换思维方向,将题设和结论都视为已知条件,进行演绎推理推导出所需寻求的条件.
5.农民收入由工资性收入和其它收入两部分构成。2003年某地区农民人均收入为3150元(其中工资性收入为1800元,其它收入为1350元), 预计该地区自2004年起的5 年内,农民的工资性收入将以每年6%的年增长率增长,其它收入每年增加160元。根据以上数据,2008年该地区农民人均收入介于( )
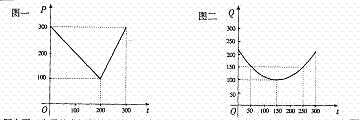 A.4200元~4400元 B.4400元~4600元 C.4600元~4800元 D.4800元~5000元
A.4200元~4400元 B.4400元~4600元 C.4600元~4800元 D.4800元~5000元
[典型考例]
[问题1] 函数应用题
[例1] P141T8 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。写出图一表示的市场售价与时间的函数关系式P=f(t)写出图二表示的种植成本与时间的函数关系式Q=g(t);认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/102kg,时间单位:天)
[例2](2004年重庆卷)某工厂生产某种产品,已知该产品的月生产量 (吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,,且生产x吨的成本为
(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,,且生产x吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
解:每月生产x吨时的利润为
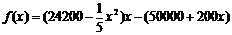
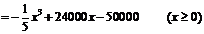
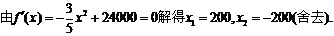
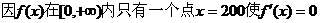 ,故它就是最大值点,
,故它就是最大值点,
且最大值为: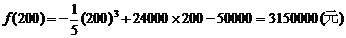
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
[针对练习1]甲方是一农场,乙方是一工厂. 由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系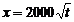 .若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格),
.若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格),
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额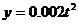 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?
(1)解法一:因为赔付价格为s元/吨,所以乙方的实际年利润为: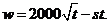
因为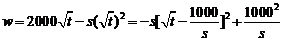 ,所以当
,所以当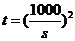 时,
时,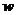 取得最大值.
取得最大值.
所以乙方取得最大年利润的年产量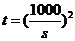 (吨).
(吨).
解法二:因为赔付价格为s元/吨,所以乙方的实际年利润为: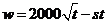 .
.
由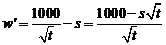 ,令
,令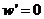 得
得 .
.
当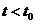 时,
时,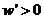 ;当
;当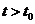 时
时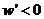 ,所以
,所以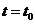 时,
时, 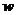 取得最大值.
取得最大值.
因此乙方取得最大年利润的年产量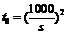 (吨).
(吨).
(2)设甲方净收入为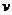 元,则
元,则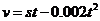 .
.
将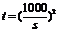 代入上式,得到甲方净收入
代入上式,得到甲方净收入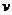 与赔付价格
与赔付价格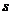 之间的函数关系式
之间的函数关系式
 .
.
又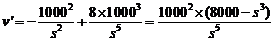 ,令
,令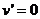 ,得
,得 .
.
当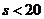 时,
时,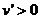 ;当
;当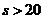 时,
时,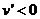 ,所以
,所以 时,
时,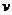 取得最大值.因此甲方向乙方要求赔付价格
取得最大值.因此甲方向乙方要求赔付价格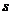
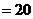 (元/吨)时,获最大净收入。
(元/吨)时,获最大净收入。
[问题1]数列应用题
[例3](P142T9)某企业2006年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从2007年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+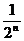 )万元(n为正整数)。(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
)万元(n为正整数)。(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
解:(Ⅰ)依题设,An=(500-20)+(500-40)+…+(500-20n)=490n-10n2;
Bn=500[(1+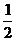 )+(1+
)+(1+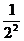 )+…+(1+
)+…+(1+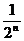 )]-600=500n-
)]-600=500n-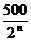 -100.
-100.
(Ⅱ)Bn-An=(500n-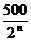 -100) -(490n-10n2)
-100) -(490n-10n2)
=10n2+10n-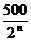 -100=10[n(n+1) -
-100=10[n(n+1) - 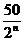 -10].
-10].
因为函数y=x(x+1) - 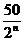 -10在(0,+∞)上为增函数,
-10在(0,+∞)上为增函数,
当1≤n≤3时,n(n+1) - 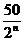 -10≤12-
-10≤12- -10<0;
-10<0;
当n≥4时,n(n+1) - 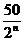 -10≥20-
-10≥20-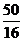 -10>0. ∴仅当n≥4时,Bn>An.
-10>0. ∴仅当n≥4时,Bn>An.
答:至少经过4年,该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.
[针对练习2]某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同.为保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
解:设2001年末汽车保有量为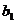 万辆,以后各年末汽车保有量依次为
万辆,以后各年末汽车保有量依次为 万辆,
万辆,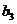 万辆,……,每年新增汽车
万辆,……,每年新增汽车 万辆,则
万辆,则 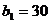 ,
,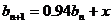 所以,当
所以,当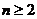 时,
时,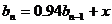 ,
,
两式相减得: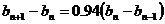
(1)显然,若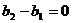 ,则
,则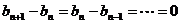 ,即
,即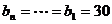 ,
,
此时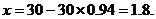
(2)若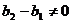 ,则数列
,则数列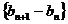 为以
为以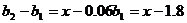 为首项,
为首项,
以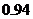 为公比的等比数列,所以,
为公比的等比数列,所以,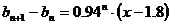 .
.
(i)若 ,则对于任意正整数
,则对于任意正整数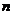 ,均有
,均有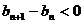 ,所以,
,所以,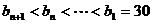 ,
,
此时,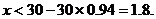
(ii)当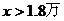 时,
时,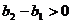 ,则对于任意正整数
,则对于任意正整数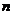 ,均有
,均有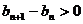 ,
,
所以, , 由
, 由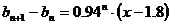 ,
,
得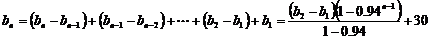
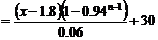 ,
,
要使对于任意正整数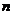 ,均有
,均有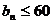 恒成立, 即
恒成立, 即 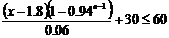
对于任意正整数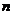 恒成立,解这个关于x的一元一次不等式 , 得
恒成立,解这个关于x的一元一次不等式 , 得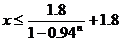 ,
,
上式恒成立的条件为: ,由于关于
,由于关于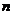 的函数
的函数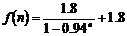 单调递减,
单调递减,
所以,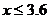 .
.
4.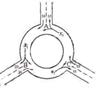 (06北京)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出
(06北京)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出
路口A,B,C的机动车辆数如图所示(20,30;35,30;55,50),图中x1,x2,x3分别表
示该时段单位时间通过路段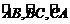 的机动车辆数(假设:单位时间内,在上述路段
的机动车辆数(假设:单位时间内,在上述路段
中,同一路段上驶入与驶出的车辆数相等),则( )
(A)x1>x2>x3 (B)x1> x3>x2, (C)x2>x3>x1> (D)x3>x1>x2
3.(04 福建)如图,将边长为1的正六边形铁皮的六个角各切去一个全等的
四边形,再沿虚线折起,做成一个无盖的正六棱柱容器。当这个正六棱柱容器的
底面边长为 2/3 时,其容积最大.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com