
15.求过点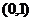 的直线,使它与抛物线
的直线,使它与抛物线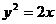 仅有一个交点。
仅有一个交点。
错误解法 设所求的过点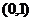 的直线为
的直线为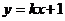 ,则它与抛物线的交点为
,则它与抛物线的交点为
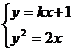 ,消去
,消去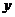 得
得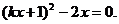 整理得
整理得 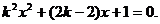
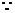 直线与抛物线仅有一个交点,
直线与抛物线仅有一个交点,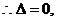 解得
解得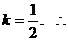 所求直线为
所求直线为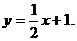
错误分析 此处解法共有三处错误:
第一,设所求直线为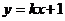 时,没有考虑
时,没有考虑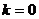 与斜率不存在的情形,实际上就是承认了该直线的斜率是存在的,且不为零,这是不严密的。
与斜率不存在的情形,实际上就是承认了该直线的斜率是存在的,且不为零,这是不严密的。
第二,题中要求直线与抛物线只有一个交点,它包含相交和相切两种情况,而上述解法没有考虑相切的情况,只考虑相交的情况。原因是对于直线与抛物线“相切”和“只有一个交点”的关系理解不透。
第三,将直线方程与抛物线方程联立后得一个一元二次方程,要考虑它的判别式,所以它的二次项系数不能为零,即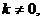 而上述解法没作考虑,表现出思维不严密。
而上述解法没作考虑,表现出思维不严密。
正确解法 ①当所求直线斜率不存在时,即直线垂直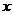 轴,因为过点
轴,因为过点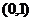 ,所以
,所以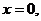 即
即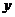 轴,它正好与抛物线
轴,它正好与抛物线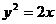 相切。
相切。
②当所求直线斜率为零时,直线为y = 1平行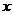 轴,它正好与抛物线
轴,它正好与抛物线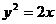 只有一个交点。
只有一个交点。
③一般地,设所求的过点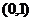 的直线为
的直线为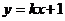
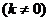 ,则
,则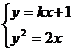 ,
,
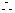
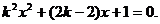 令
令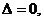 解得k = ,∴ 所求直线为
解得k = ,∴ 所求直线为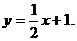
综上,满足条件的直线为: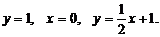
14.曲线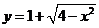 ,与直线
,与直线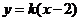 有两个公共点,则实数k取值范围是(
)
有两个公共点,则实数k取值范围是(
)
A. 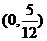 B.
B. 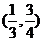 C.
C. 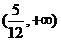 D.
D. 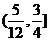
析:错选C,错因化一元二次方程求解,忽视了函数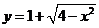 的特点,解题策略不当,应注意数形结合,用直线和圆珠笔的位置关系求解。
的特点,解题策略不当,应注意数形结合,用直线和圆珠笔的位置关系求解。
[错误形式3]重视一般性,忘记特殊性
13.已知:a>0 , b>0 , a+b=1,求(a+ )2+(b+ )2的最小值。
错解 (a+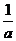 )2+(b+
)2+(b+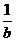 )2=a2+b2+
)2=a2+b2+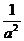 +
+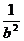 +4≥2ab+
+4≥2ab+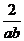 +4≥4
+4≥4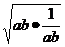 +4=8,
+4=8,
∴(a+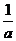 )2+(b+
)2+(b+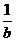 )2的最小值是8.
)2的最小值是8.
分析 上面的解答中,两次用到了基本不等式a2+b2≥2ab,第一次等号成立的条件是a=b=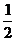 ,第二次等号成立的条件是ab=
,第二次等号成立的条件是ab=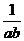 ,显然,这两个条件是不能同时成立的。因此,8不是最小值。
,显然,这两个条件是不能同时成立的。因此,8不是最小值。
事实上,原式= a2+b2+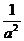 +
+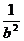 +4=( a2+b2)+(
+4=( a2+b2)+(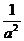 +
+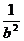 )+4=[(a+b)2-2ab]+[(
)+4=[(a+b)2-2ab]+[(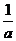 +
+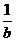 )2-
)2-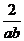 ]+4
]+4
=
(1-2ab)(1+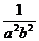 )+4,
)+4,
由ab≤( )2=
)2=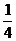 得:1-2ab≥1-
得:1-2ab≥1-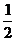 =
=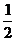 , 且
, 且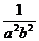 ≥16,1+
≥16,1+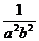 ≥17,
≥17,
∴原式≥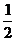 ×17+4=
×17+4=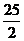 (当且仅当a=b=
(当且仅当a=b=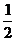 时,等号成立),
时,等号成立),
∴(a + 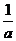 )2 + (b +
)2 + (b + 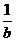 )2的最小值是。
)2的最小值是。
12.已知{(x,y)|(m+3)x+y=3m-4}∩{(x,y)|7x+(5-m)y-8=0}=φ则直线(m+3)x+y=3m+4与坐标轴围成的三角形的面积是
析:只重平行,忽视重合,忘舍了m=4
[错误形式2]忽视不等式中等号成立的条件,导致结果错误。
11.设O(0,0)A(1,0),B(0,1)P是线段AB上的一个动点,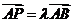 若
若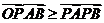 则实数
则实数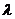 取值范围是( )A.
取值范围是( )A.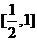 B.
B.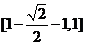 C.
C.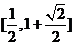 D.
D.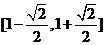
析:忽视了点P在线段AB上应满条件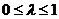 ,错选了D,应选B
,错选了D,应选B
10.直线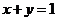 与圆
与圆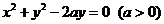 没有公共点,则实数
没有公共点,则实数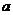 取值范围是( )
取值范围是( )
A.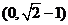 B.
B.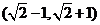 C.
C.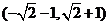 D.
D.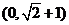
析:应选A,忽视了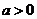 ,错误地选取了C。
,错误地选取了C。
9.在极坐标系中,从极点O作圆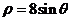 的弦ON,则ON的中点的轨迹方程是
的弦ON,则ON的中点的轨迹方程是
析: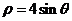 ,错误原因是写成了直角坐标系内的方程
,错误原因是写成了直角坐标系内的方程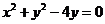
8.在函数y=x3-8x的图象上,其切线的倾斜角小于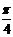 的点中,坐标为整数的点的个数是
的点中,坐标为整数的点的个数是
A.3 B.2 C.1 D.0
析:(忽视了倾角的定义与斜率之间的关系,即导数限制条件是: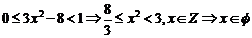 )
)
7.已知椭圆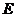 :
: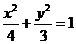 的两个焦点分别为
的两个焦点分别为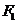 、
、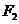 ,若点
,若点 在椭圆
在椭圆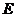 上,且满足
上,且满足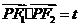 ,求实数
,求实数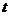 的取值范围.
的取值范围.
6. 已知(x+2)2+ =1, 求x2+y2的取值范围。
错解 由已知得 y2=-4x2-16x-12,因此 x2+y2=-3x2-16x-12=-3(x+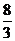 )2+
)2+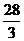 ,
,
∴当x=-时,x2+y2有最大值,即x2+y2的取值范围是(-∞, ]。
分析 没有注意x的取值范围要受已知条件的限制,丢掉了最小值。
事实上,由于(x+2)2+ =1 Þ (x+2)2=1- ≤1 Þ -3≤x≤-1,
从而当x=-1时x2+y2有最小值1。∴ x2+y2的取值范围是[1, ]。
注意有界性:偶次方x2≥0,三角函数-1≤sinx≤1,指数函数ax>0,圆锥曲线有界性等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com