
21.(本题满分13分)
设函数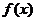
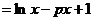 .
.
(1)求函数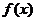 的极值点;
的极值点;
(2)当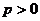 ,若对任意的
,若对任意的 ,恒有
,恒有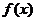 ≤0,求
≤0,求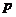 的取值范围;
的取值范围;
(3)证明: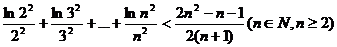 .
.
19.(本题满分13分)
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(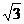 ,0).
,0).
(1)求双曲线C的方程;
(2)若直线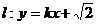 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且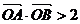 (其中O为原点),求
(其中O为原点),求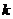 的取值范围。
的取值范围。
18.(本题满分12分)
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,
EC⊥AC,EF∥AC,AB=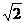 ,EF=EC=1。
,EF=EC=1。
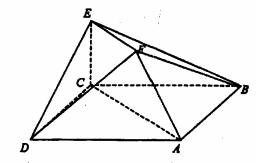 (1)求证:EC∥平面BFD;
(1)求证:EC∥平面BFD;
(2)求证:DF⊥EF;
(3)求二面角B-EF-D的大小。
17.(本题满分12分)
有一高二升高三的学生盼望进入某名牌大学学习,假设该名牌大学由以下每种方式都可录取:①2010年2月国家数学奥赛集训队考试通过(集训队从2009年10月省数学竞赛一等奖中选拔);②2010年3月自主招生考试通过并且2010年6月高考分数达重点线;③2010年6月高考达到该校录取分数线(该校录取分数线高于重点线)。该考生具有参加省数学竞赛、自主招生和高考的资料且估计自己通过各种考试的概率如下表:
|
省数学竞赛获一等奖 |
自主招生通过 |
高考达重点线 |
高考达该校分数线 |
|
0.5 |
0.7 |
0.8 |
0.6 |
如果数学竞赛获省一等奖,该学生估计自己进入国际集训队的概率是0.4.若进入国家集训队,则提前录取,若未被录取,则再按②,③顺序依次录取;前面已经被录取后,不得参加后面的考试或录取。
(1)求该考生参加自主招生考试的概率;
(2)求该学生参加考试的次数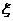 的分布列及数学期望;
的分布列及数学期望;
(3)求该学生被该校录取的概率。
16.(本题满分12分)
在△ABC中,角A、B、C所对的边分别为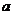 、
、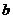 、
、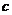 ,且
,且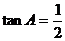 ,
,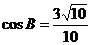 .
.
(1)求tanC的值;
(2)若△ABC最长的边为1,求b。
15.已知函数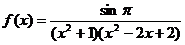
(Ⅰ)方程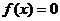 在区间
在区间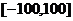 上实数解的个数是
;
上实数解的个数是
;
(Ⅱ)对于下列命题:①函数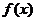 是周期函数;
是周期函数;
②函数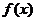 既有最大值又有最小值;
既有最大值又有最小值;
③函数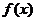 的定义域是R,且其图象有对称轴;
的定义域是R,且其图象有对称轴;
④对于任何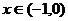 ,
,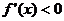 ,(
,(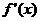 是函数
是函数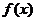 的导函数)
的导函数)
其中真命题的序号是 。(填写处所有真命题的序号)
14.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数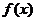 的图象恰好通过
的图象恰好通过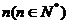 个整点,则称函数
个整点,则称函数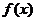 为
为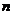 阶整点函数,有下列函数
阶整点函数,有下列函数
①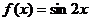 ②
②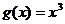 ③
③ ; ④
; ④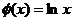 ,
,
其中是一阶整点函数的是 。(写出所有正确结论的序号)
13.现有一个关于平面图形的命题:如图所示,同一个平
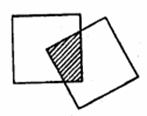 面内有两个边长都是
面内有两个边长都是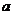 的正方形,其中一个的某顶点
的正方形,其中一个的某顶点
在另一个的中心,则这两个正方形重叠部分的面积恒为
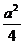 ,类比到空间,有两个棱长均为
,类比到空间,有两个棱长均为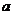 的正方形,其中
的正方形,其中
一个的某顶点在另一个的中心,则这两个正方体重叠部分
的体积恒为 。
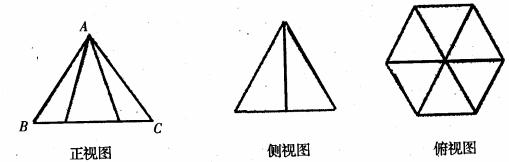
12.一个几何体的三视图如图所示:其中,正视图△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体的体积为 。
11.设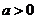 ,
,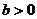 。若
。若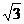 是
是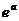 与
与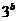 的等比中项,则
的等比中项,则
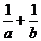 的最小值为
。
的最小值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com