3.解决匀速圆周运动问题的一般方法

(1)明确研究对象，必要时将它从转动系统中隔离出来。

(2)找出物体圆周运动的轨道平面，从中找出圆心和半径。

(3)分析物体受力情况，千万别臆想出一个向心力来。

(4)建立直角坐标系(以指向圆心方向为x轴正方向)将力正交分解。

(5)

2.特例(1)火车转弯：设火车弯道处内外轨高度差为h，内外轨间距L，转弯半径R。由于外轨略高于内轨，使得火车所受重力和支持力的合力F_合提供向心力。

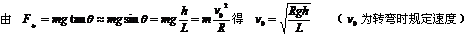
①当火车行驶速率V等于V₀时，F_合=F_向，内外轨道对轮缘都没有侧压力

②当火车行驶V大于V₀时，F_合<F_向，外轨道对轮缘有侧压力，F_合+N=mv²/R

③当火车行驶速率V小于V₀时，F_合>F_向，内轨道对轮缘有侧压力，F_合-N'=mv²/R

即当火车转弯时行驶速率不等于V₀时，其向心力的变化可由内外轨道对轮缘侧压力自行调节，但调节程度不宜过大，以免损坏轨道。

(2)水流星模型(竖直平面内的圆周运动)

没有物体支撑的小球，在竖直平面做圆周运动过最高点的情况：注意：绳对小球只能产生沿绳收缩方向的拉力

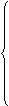①临界条件：由mg+T=mv²/L知，小球速度越小，绳拉力或环压力T越小，但T的最小值只能为零，此时小球以重力为向心力，

结论：恰能通过最高点：绳子或轨道对小球没有力的作用：mg=mv²/R→v_临界=(可理解为恰好转过或恰好转不过的速度)

②能过最高点条件：V≥V_临=　 (当V≥V_临时，绳、轨道对球分别产生拉力、压力)

③不能过最高点条件：V<V_临　　　 (实际上球还未到最高点就脱离了轨道)

讨论：① 恰能通过最高点时：mg=，临界速度V_临=；

☆可认为距此点 (或距圆的最低点)处落下的物体。

☆此时最低点需要的速度为V_低临=　 　☆最低点拉力大于最高点拉力ΔF=6mg

② 最高点状态: mg+T₁= (临界条件T₁=0, 临界速度V_临=, V≥V_临才能通过)

最低点状态: T₂- mg = 　　　高到低过程机械能守恒:

最低点与最高点拉力之差：T₂- T₁=6mg(g可看为等效加速度)

③半圆：过程mgR= 最低点T-mg= 绳上拉力T=3mg； 过低点的速度为V_低 =　

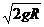
小球在与悬点等高处静止释放运动到最低点，最低点时的向心加速度a=2g

④与竖直方向成q角下摆时,过低点的速度为V_低 =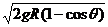, 此时绳子拉力T=mg(3-2cosq)

(3)有支承的小球，在竖直平面作圆周运动过最高点情况，

轻质杆(管)对球产生的弹力情况：注意：杆与绳不同，杆对球既能产生拉力，也能对球产生支持力．

临界条件：杆和环对小球有支持力的作用　

①当V=0时，N=mg (N为支持力) (可理解为小球恰好转过或恰好转不过最高点)

恰好过最高点时，此时从高到低过程 mg2R=1/2mv² 　低点：T-mg=mv²/R 　T=5mg

恰好过最高点时，此时从高到低过程 mg2R=　

低点：T-mg=mv²/R ☆ T=5mg ；恰好过最高点时，此时最低点速度：☆V_低 =

注意：充分理解

①管壁支撑情况与杆子一样。

②若是通过圆弧轨道的最高点有一速度,先讨论是否V≥V_临，若是将脱离轨道做平抛运动．因为轨道对小球不能产生拉力．

③如果小球带电,且空间存在电场或磁场时,临界条件应是小球所受重力、电场力和洛仑兹力的合力等于向心力,此时临界速度 。要具体问题具体分析，但分析方法是相同的。

④物理圆与几何圆的最高点、最低点的区别 (以上规律适用于物理圆,不过最高点,最低点, g都应看成等效的)

1.圆周运动中的临界问题的分析方法

首先明确物理过程，对研究对象进行正确的受力分析，然后确定向心力，根据向心力公式列出方程，由方程中的某个力的变化与速度变化的对应关系，从而分析找到临界值．

竖直平面内的圆周运动是典型的变速圆周运动。研究物体通过最高点和最低点的情况,并且经常出现临界状态。(圆周运动实例)

①火车转弯

②汽车过拱桥、凹桥₃

③飞机做俯冲运动时，飞行员对座位的压力。

④物体在水平面内的圆周运动 (汽车在水平公路转弯，水平转盘上的物体，绳拴着的物体在光滑水平面上绕绳的一端旋转)和

物体在竖直平面内的圆周运动(翻滚过山车、水流星、杂技节目中的飞车走壁等)。

⑤万有引力--卫星的运动、库仑力--电子绕核旋转、洛仑兹力--带电粒子在匀强磁场中的偏转、重力与弹力的合力--锥摆、

(关健要搞清楚向心力怎样提供的)

4、圆周运动中实例分析

　　　　　　 圆周运动的应用专题

3、圆周运动与其它运动的结合

圆周运动和其他运动相结合，要注意寻找这两种运动的结合点：如位移关系、速度关系、时间关系等．

还要注意圆周运动的特点：如具有一定的周期性等．

点评：对于比较复杂的问题，一定要注意分清物理过程，而分析物理过程的前提是通过分析物体的受力情况进行．

2．向心力的认识和来源

(1)向心力是根据力的效果命名的，不是和重力、弹力、摩擦力相并列的一种类型的力．在分析做圆周运动的质点受力情况时，切不可在物体的相互作用力(重力、弹力、摩擦力、万有引力)以外再添加一个向心力．

(2)物体做匀速圆周运动的条件是：物体的合外力大小不变，方向始终与速度方向垂直且指向圆心。

由于匀速圆周运动仅是速度方向变化而速度大小不变的运动，故只存在向心加速度，物体受的外力的合力就是向心力。显然

(3)分析向心力来源的步骤是:首先确定研究对象运动的轨道平面和圆心的位置，然后分析圆周运动物体所受的力,作出受力图,最后找出这些力指向圆心方向的合外力就是向心力．

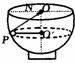
例如，沿半球形碗的光滑内表面，一小球在水平面上做匀速圆周运动，如图小球做圆周运动的圆心在与小球同一水平面上的O^/点，不在球心O，也不在弹力N所指的PO线上．

这种分析方法和结论同样适用于圆锥摆、火车转弯、飞机在水平面内做匀速圆周飞行等在水平面内的匀速圆周运动的问题。共同点是由重力和弹力的合力提供向心力，向心力方向水平。

(4)变速圆周运动向心力的来源：分析向心力来源的步骤同分析匀速圆周运动向心力来源的步骤相向．但要注意，

①一般情况下，变速圆周运动的向心力是合外为沿半径方向的分力提供．

②分析竖直面上变速圆周运动的向心力的来源时，通常有细绳和杆两种模型．

(5)当物体所受的合外力小于所需要提供的向心力时，即F_向＜时，物体做离心运动；

当物体所受的合外力大于所需要的向心力，即F_向＞时，物体做向心运动。

每1/30秒更一帧，车上有8根对称辐条，若在1/30秒内，每根辐条恰好转过角度为

45、360、365、355)观众觉得车轮是怎样转的。(45度时不动；360时不动、355度倒转)。

规律方法　 1.线速度、角速度、向心加速度大小的比较

在分析传动装置的各物理量时．要抓住不等量和相等量的关系．

①同轴的各点角速度ω和n相等，而线速度v＝ωr与半径r成正比．

②在不考虑皮带打滑的情况下．传动皮带与皮带连接的两轮边缘的各点线速度大小相等，而角速度ω＝v/r与半径r成反比．

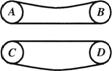
[例1]对如图所示的皮带传动装置，下列说法中正确的是

(A)A轮带动B轮沿逆时针方向旋转．(B)B轮带动A轮沿逆时针方向旋转．

(C)C轮带动D轮沿顺时针方向旋转．(D)D轮带动C轮沿顺时针方向旋转．

[例3]如图所示，直径为d的纸质圆筒，以角速度ω绕轴O高速运动，有一颗子弹沿直径穿过圆筒，若子弹穿过圆筒时间小于半个周期，在筒上先、后留下a、b两个弹孔，已知ao、bo间夹角为φ弧度，则子弹速度为 　　　　　　

1．灵活、正确地运用公式 ΣF_n＝ma_n=mv²/r＝mω²r＝m4π²r/T²＝m4π²fr ；2．正确地分析物体的受力情况，找出向心力．

变速圆周运动的物体，不仅线速度大小、方向时刻在改变，而且加速度的大小、方向也时刻在改变，是变加速曲线运动

(注：匀速圆周运动也是变加速运动)．

变速圆周运动的合力一般不指向圆心，变速圆周运动所受的合外力产生两个效果．

①半径(法向)方向的分力：产生向心加速度，而改变速度方向快慢的物理量。法向加速度。

②切线方向的分力：产生切线方向加速度而改变速度大小．切向加速度

故利用公式求圆周上某一点的向心力和向心加速度的大小，必须用该点的瞬时速度值．

4．质点做匀速圆周运动的条件：质点具有初速度，并且始终受到方向与线速度方向垂直，时刻指向圆心的大小不变的合外力(即向心力)作用