102、最不后悔的活法

　泰莱是纽约曼哈顿区的一位神父。

　那天，教区医院里一位病人生命垂危，他被请过去主持临终前的忏悔。他到医院后听到这样一段话：“仁慈的上帝！我喜欢唱歌，音乐是我的生命，我的愿望是唱遍美国。作为一名黑人，我实现了这个愿望，我没有什么要忏悔的，现在我只想说，感谢您，您让我愉快地度过了一生，并让我用歌声养活了我的6个孩子。正在我的生命就要结束了，但死而无憾。仁慈的神父，现在我只想请您转告我的孩子，让他们做自己喜欢做的事吧，他们的父亲是会为他们骄傲的。”

　一个流浪歌手，临终时能说出这样的话，让泰莱神父感到非常吃惊，因为这名黑人歌手的所有家当，就是一把吉他。他的工作是每到一处，就把头上的帽子放在地上，开始唱歌。40年来，他如痴如醉，用他苍凉的西部歌曲，感染他的听众，从而换取那份他应得的报酬。

　黑人的话让神父想起5年前曾主持过的一次忏悔。那是位富翁，他的忏悔竟然和这痊黑人流浪汉差不多。他对神父说，我喜欢赛车，我从小研究它们、改进它们、经营它们，一辈子都都没有离开过它们。这种工作和爱好难分、闲暇与兴趣结合的生活，让我非常满意，并且从中还赚取了大笔的钱，我没有什么要忏悔的。

　白天的经历和对对那位富翁的回忆，让泰莱神父陷入思索。当晚，他给纽约时报去了一封信。信里写道：“人应该怎样度过自己的一生才不会留下悔恨呢？我想也许做到两条就够了。第一条，做自己喜欢的事；第二条，想办法从中赚到钱。”

　后来，泰莱神父的这两条生活信条，成了美国人公认的最不后悔的活法。

101、给生命加压

　一艘货轮在空船返航途中，在浩淼的大海上，突然遭遇特大风暴。

　货轮在暴风雨中不停地摇晃着、颠簸着，水手们惊惶失措，只有老船长镇静地指挥着：“打开所有货舱，立刻往里面灌水。”

　水手们更加不安和不解：“往船里灌水不是自找死路吗？”

　船长镇定地说：“大家见过根深干粗的树被暴风刮倒过吗？被刮倒的是没有根基的小树。”

　水手们半信半疑地照着做了。虽然暴风巨浪依旧那么激烈，但随着货舱里的水位越来越高，货轮渐渐平稳了。

　船长告诉那些松了一口气的水手：“一只空木桶，是很容易被风打翻的，如果装满水负重了，风是吹不倒的。船在负重的时候，是最安全的；空船时，才是最危险的时候。”

100、机会只有三秒

　她名牌大学毕业，却找不到工作，好不容易找了份戏剧编剧助理的工作，累死累活干了3个月，只拿到一个月的工资，于是炒了老板的鱿鱼。开始游荡，帮人写短剧，写电影，只要按时收到钱就好，前途茫茫，她希望发生奇迹。

　一次机缘巧合，她就聘到电视台一个节目当了编剧。半年后，一次在制作节目时，制作人不知为什么突然大发雷霆，说了句“不录了”就走了。几十个工作人员全愣在那儿，不知怎么办？主持人对她说：“下面的我们自己录吧！”

　3秒钟后，她拿起制作人丢下的耳机和麦克风。那一刻，她清楚地对自己说：“这一次如果成功了，就证明你不仅是一个只会写写小剧本的小编剧，还可以是一个掌控全场的制作人，所以不能出丑！”

　慢慢地，她开始做执行制作人，当时，像她那个年纪的女生做制作人的情况相当罕见。几年后，这个小女生成了三度获得金钟奖的王牌制作人，接着一手制作了红得一塌糊涂的电视剧《流星花园》，被称为台湾偶像剧之母。

回首往事，柴智屏爽直地说：“机会只有3秒，就是在别人丢下耳机和麦克风的时候，你能捡起它。”

20．(本小题共13分)

已知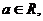函数．

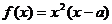(1)当a=3时，求f(x)的零点；

(2)求函数y＝f (x)在区间[1,2]上的最小值．

　　　　　　 　广东省广州市重点中学2010届高三12月月考

19．(本小题共14分)

已知二次函数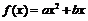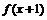，为偶函数，函数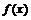的图象与直线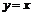相切．

(1)求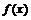的解析式；

(2)若函数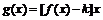在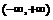上是单调减函数，那么：求k的取值范围；

18．(本小题满分14分)

在平面直角坐标系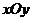，已知圆心在第二象限、半径为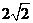的圆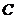与直线y=x相切于坐标原点O。椭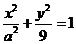圆与圆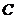的一个交点到椭圆两焦点的距离之和为。

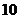(1)求圆C的方程；

(2)在圆C上存在异于原点的点Q，使Q到椭圆右焦点F的距离等于线段OF的长，请求出Q点的坐标

17．(本小题共14分)

在长方形ABEF中，D,C分别是AF和BE的中点，M和N分别是AB和AC的中点，AF=2AB=2a,将平面DCEF沿着DC折起，使角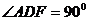，G是DF上一动点

求证：

⑴GN垂直AC

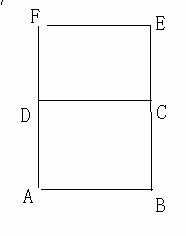⑵当FG=GD时，求证：GA||平面FMC。

15．(本小题共12分)

已知△ABC顶点的直角坐标分别为A(3，4)，B(0，0)，C(c，0)

(1)若c=5，求sin∠A的值；

(2)若∠A是钝角，求c的取值范围。

16(本小题满分12分)

在数列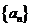中，，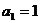

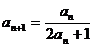
I)求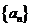的通项公式。

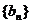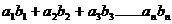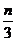II)若数列满足=，求数列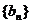的通项公式

14．已知函数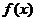，分别由下表给出

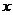	1	2	3
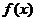	1	3	1

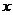	1	2	3
	3	2	1

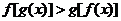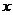则满足的的值是　　　　　　　　　　　　　 。

13、圆截直线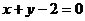所得的弦长等于　　　　　　　　　　　　　 。