
15.(本小题满分12分)
已知函数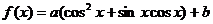
(1)当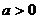 时,求
时,求 的单调递增区间;
的单调递增区间;
(2)当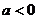 且
且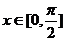 时,
时, 的值域是
的值域是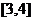 ,求
,求 的值。
的值。
16.(本小题满分12分)
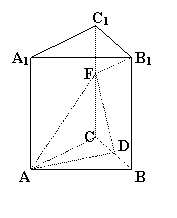 在三棱柱
在三棱柱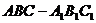 中,
中,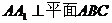
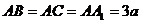 ,
,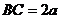 ,
, 是
是 的中点,F是
的中点,F是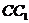 上一点,且
上一点,且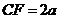 .
.
(1) 求证: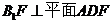 ;
;
(2) 求平面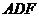 与平面
与平面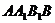 所成角的正弦值.
所成角的正弦值.

17.(本小题满分14分)
某自来水厂的蓄水池有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水, 小时内供水总量为
小时内供水总量为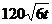 吨,其中
吨,其中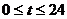 。
。
(1) 从供水开始到第几小时,蓄水池中的存水量最少?最少水量是多少吨?
(2) 若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象。
18.(本小题满分14分)
已知椭圆的中心为坐标原点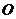 ,焦点在
,焦点在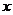 轴上,斜率为1且过椭圆右焦点
轴上,斜率为1且过椭圆右焦点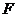 的直线交椭圆于
的直线交椭圆于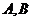 两点,
两点, 与
与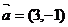 共线。
共线。
(1) 求椭圆的离心率;
(2) 设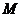 为椭圆上任意一点,且
为椭圆上任意一点,且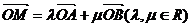 ,证明
,证明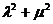 为定值。
为定值。
19.(本小题满分14分)
设函数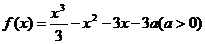 。
。
(1) 如果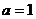 ,点
,点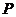 为曲线
为曲线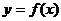 上一个动点,求以
上一个动点,求以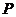 为切点的切线斜率取最小值时的切线方程;
为切点的切线斜率取最小值时的切线方程;
(2) 若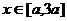 时,
时, 恒成立,求
恒成立,求 的取值范围。
的取值范围。
20.(本小题满分14分)
设函数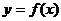 定义域为
定义域为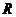 ,当
,当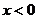 时,
时,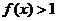 ,且对于任意的
,且对于任意的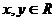 ,都有
,都有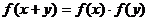 成立,数列
成立,数列 满足
满足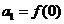 ,且
,且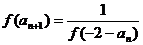 。
。
(1) 求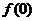 的值,并证明函数
的值,并证明函数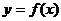 在
在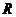 上是减函数;
上是减函数;
(2) 求数列 的通项公式并证明;
的通项公式并证明;
(3) 是否存在正数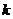 ,使
,使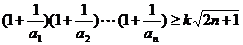 对一切
对一切 都成立,若存在,求出
都成立,若存在,求出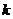 的最大值,并证明,否则说明理由。
的最大值,并证明,否则说明理由。
14、▲选做题:在下面三道题中选做两题,三题都选的只计算前两题的得分。
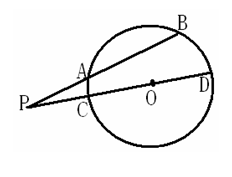
(1)已知⊙O的割线PAB交⊙O于A,B两点,
割线PCD经过圆心,若PA=3,AB=4,PO=5,
则⊙O的半径为_______________
(2)已知直线的极坐标方程为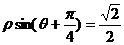 ,则点A
,则点A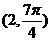 到这条直线的距离为_____________
到这条直线的距离为_____________
(3)若关于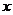 的不等式
的不等式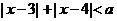 的解集不是空集,则参数
的解集不是空集,则参数 的取值范围是 。
的取值范围是 。
13.对任意两个集合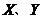 ,定义
,定义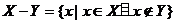 ,
,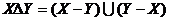
设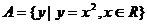 ,
,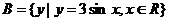 ,则
,则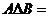 __ __。
__ __。
12.设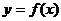 是可导函数,且满足
是可导函数,且满足 则曲线
则曲线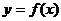 上以点
上以点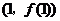 为切点的切线倾斜角
为切点的切线倾斜角 为 __ __。
为 __ __。
11.已知数列 满足
满足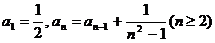 ,则
,则 的通项公式为_ _。
的通项公式为_ _。
10.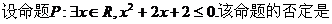 __
__。
__
__。
9.用秦九韶算法求多项式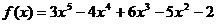 ,当
,当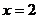 时的值,需要进行 次乘法运算及 次加(减)法运算。
时的值,需要进行 次乘法运算及 次加(减)法运算。
8.设函数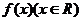 为奇函数,
为奇函数, ,
,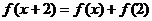 ,则
,则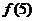 =
=
A. 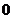 B. 1 C.
B. 1 C.
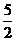 D. 5
D. 5
7.已知函数 表示的曲线过原点,且在
表示的曲线过原点,且在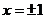 处的切线斜率均为-1,有以下命题
处的切线斜率均为-1,有以下命题
①f(x)的解析式为:f(x)=x3-4x,x∈[-2,2];
②f(x)的极值点有且仅有一个;
③f(x)的最大值与最小值之和等于零;
其中正确的命题个数为
A. 0 B. 1 C. 2 D. 3
6. 设向量 ,向量
,向量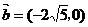 ,则
,则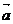 与
与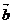 的夹角是
的夹角是
A. 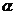 B.
B. 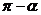 C.
C. 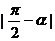 D.
D. 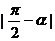
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com