4.应用：①可直观地读取振幅A、周期T以及各时刻的位移x；

②判定各时刻的回复力、速度、加速度方向；

③判定某段时间内位移、回复力、加速度、速度、动能、势能、等物理量的变化情况

注意：①振动图象不是质点的运动轨迹．

②计时点一旦确定，形状不变，仅随时间向后延伸。

③简谐运动图像的具体形状跟计时起点及正方向的规定有关。

规律方法1、简谐运动的特点 2、弹簧振子模型

3.特点：简谐运动的图象是正弦(或余弦)曲线．

2.坐标系：以横轴表示时间，纵轴表示位移，用平滑曲线连接各时刻对应的位移末端即得

1.物理意义：表示振动物体(或质点)的位移随时间变化的规律．

说明:简谐运动的位移,回复力,加速度,速度都随时间做周期性变化(正弦或余弦函数)变化周期为T,振子的动能、势能也做周期性变化,周期为T/2

①凡离开平衡位置的过程，v、E_k均减小，x、F、a、E_P均增大；凡向平衡位置移动时，v、E_k均增大, x、F、a、E_P均减小.

②振子运动至平衡位置时，x、F、a为零，E_P最小，v、E_k最大；当在最大位移时，x、F、a、E_P最大，v、E_k最为零；

③在平衡位置两侧的对称点上,x、F、a、v、E_k、E_P的大小均相同．

4、在水平方向上振动的弹簧振子的回复力是弹簧的弹力；在竖直方向上振动的弹簧振子的回复力是弹簧弹力和重力的合力。

3、可以证明，竖直放置的弹簧振子的振动也是简谐运动，周期公式也是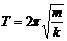。这个结论可以直接使用。

2、弹簧振子振动周期：T=2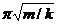，只由振子质量和弹簧的劲度决定，与振幅无关，也与弹簧振动情况无关。

(如水平方向振动或竖直方向振动或在光滑的斜面上振动或在地球上或在月球上或在绕地球运转的人造卫星上)

1、一个可作为质点的小球与一根弹性很好且不计质量的弹簧相连组成一个弹簧振子．一般来讲，弹簧振子的回复力是弹力(水平的弹簧振子)或弹力和重力的合力(竖直的弹簧振子)提供的．弹簧振子与质点一样，是一个理想的物理模型．

2、简谐振动：物体所受的回复力跟位移大小成正比时，物体的振动是简偕振动．

①受力特征：回复力F=-KX。②运动特征：加速度a=一kx／m，方向与位移方向相反，总指向平衡位置。

简谐运动是一种变加速运动，在平衡位置时，速度最大，加速度为零；在最大位移处，速度为零，加速度最大。

说明：①判断一个振动是否为简谐运动的依据是看该振动中是否满足上述受力特征或运动特征。

②简谐运动中涉及的位移、速率、加速度的参考点，都是平衡位置.