8．弧长公式：l ＝　　　　　　　　 ；

扇形面积公式：S＝　　　　　　 .

7．弧度与角度互化：180º＝　　　 弧度，1º＝　　 　弧度，1弧度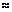＝　　　 　　　　　º．

6．弧度制的意义：圆周上弧长等于半径长的弧所对的圆心角的大小为1弧度的角，它将任意角的集合与实数集合之间建立了一一对应关系．

5．区间角是指：　　　　　　　　　 ．

4．象限角是指：　　　　　　　　　 ．

3．轴线角(终边在坐标轴上的角)

终边在x轴上的角的集合为　　　 ，终边在y轴上的角的集合为　　　 ，终边在坐标轴上的角的集合为　　　　　 ．

2．与角终边互为反向延长线的角的集合为　　　　　　 ．

1．与角终边相同的角的集合为　　　　　　　 ．

5、结构辩证语言的小技巧：在某一段文字里，如果你要达到辩证说理的效果，需要一点结构语言的小技巧，比如，你能用下面的词语说一段话吗？“诚然(确实)……不过……虽说……但是……其实……总之……”试一试，你会发现，你的观点辩证多了。

[请你试写]

有这样一件事：大学毕业多年后，某个班的同学相约来到老师家，一阵寒暄之后，大家纷纷向老师大倒苦水，觉得工作压力大，对自己的生活大发牢骚。老师没有说一句话，他让大家自己取杯子冲咖啡，老师家的杯子各式各样，大家挑选着自己喜欢的杯子冲泡咖啡，冲完咖啡后，老师说：“不知大家注意到没有，那些外观精美的杯子被你们拿走了，剩下的都是不起眼的杯子。人人都想把最好的留给自己，但这正是生活中问题和压力的根源，你们真正要的是咖啡，不是咖啡杯。可是大家不约而同地把好看的杯子拿走，并且还看别人的杯子是否比自己的好看。”老师的一席话，让大家陷入了深思。

读了这个故事后，你有什么感触呢？请自拟题目，自设立意，写一篇不少于800字的文章。特别要求：语言的辩证性。

4、转折与例证：为了使自己的观点更具有说服力，作者常常用“正－转－例－析”议论更全面，更辩证。比如：“张扬自己的青春，人生才会灿烂多彩。然而过于张扬就成了张狂。张狂是幼稚的表现，它可能会让你跌入万丈深渊。韩信点兵，多多益善。面对着刘邦别有用意的提问，韩信低头看着棋局，漫不经心地回答。在关键时刻，他不懂得内敛，依然口出狂言。殊不知他这句话更加坚定了刘邦要灭掉他的决心。张狂使他将自己推向死亡。我们要懂得在张扬中学会内敛。”作者先说“张扬”的好处，然后来一个转折，接着举例论证，最后一句点评，表达自己的观点，这样的论证是否比单纯地论证“张扬”的好处更全面呢？