
4.诱导公式的作用:
诱导公式可以将求任意角的三角函数值转化为0°~90º角的三角函数值.
|
例1. 已知f( )=
)=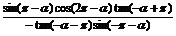 ;
;
(1)化简f( );
);
(2)若 是第三象限角,且cos
是第三象限角,且cos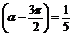 ,求f(
,求f( )的值.
)的值.
解
:(1)f( )=
)=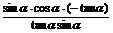 =-cos
=-cos .
.
(2)∵cos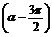 =-sin
=-sin ,
,
∴sin =-
=-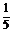 ,cos
,cos =-
=-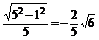 ,
,
∴f( )=
)=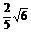 .
.
变式训练1:已知A=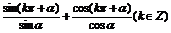 则A构成的集合是 ( )
则A构成的集合是 ( )
A.{-1, 1, -2, 2} B.{1, -1}
C.{2, -2} D.{-2, -1, 01, 2}
解:C
例2.求值:(1) 已知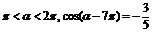 ,求
,求 的值.
的值.
2) 已知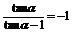 ,求下列各式的值.①
,求下列各式的值.①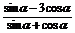 ;②
;②
解:(1)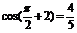 ;
;
(2)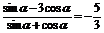
变式训练2:化简:① 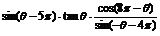 , ②
, ② 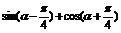
解:①原式=sinθ ② 原式=0
例3. 已知-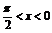 ,sin x+cos x=
,sin x+cos x=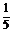 .
.
(1)求sin x-cos x的值.
(2)求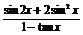 的值.
的值.
解:( 1 ) -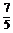 ,( 2 ) -
,( 2 ) -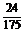
变式训练3:已知sin +cos
+cos =
=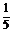 ,
, ∈(0,
∈(0, ).求值:
).求值:
(1)tan ;(2)sin
;(2)sin -cos
-cos ;(3)sin3
;(3)sin3 +cos3
+cos3 .
.
解 方法一 ∵sin +cos
+cos =
=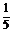 ,
, ∈(0,
∈(0, ),
),
∴(sin +cos
+cos )2=
)2=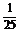 =1+2sin
=1+2sin cos
cos ,
,
∴sin cos
cos =-
=- <0.
<0.
由根与系数的关系知,
sin ,cos
,cos 是方程x2-
是方程x2-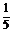 x-
x- =0的两根,
=0的两根,
解方程得x1=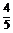 ,x2=-
,x2=-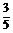 .
.
∵sin >0,cos
>0,cos <0,∴sin
<0,∴sin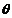 =
=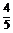 ,cos
,cos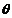 =-
=-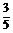 .
.
∴(1)tan =-
=-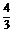 .
.
(2)sin
 -cos
-cos =
=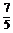 .
.
(3)sin3 +cos3
+cos3 =
=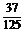 .
.
方法二 (1)同方法一.
(2)(sin -cos
-cos )2=1-2sin
)2=1-2sin ·cos
·cos
=1-2×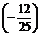 =
=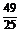 .
.
∵sin >0,cos
>0,cos <0,∴sin
<0,∴sin -cos
-cos >0,
>0,
∴sin -cos
-cos =
=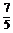 .
.
(3)sin3 +cos3
+cos3 =(sin
=(sin +cos
+cos )(sin2
)(sin2 -sin
-sin cos
cos +cos2
+cos2 )
)
=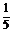 ×
×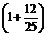 =
=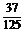 .
.
例4.已知tan =2,求下列各式的值:
=2,求下列各式的值:
(1)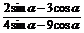 ;
;
(2) 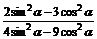 ;
;
(3)4sin2 -3sin
-3sin cos
cos -5cos2
-5cos2 .
.
解:(1)原式=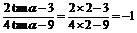 .
.
(2)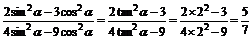 .
.
(3)∵sin2 +cos2
+cos2 =1,
=1,
∴4sin2 -3sin
-3sin cos
cos -5cos2
-5cos2
=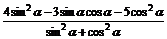 [来源:]
[来源:]
= .
.
变式训练4:已知sin( +k
+k )=-2cos(
)=-2cos( +k
+k ) (k∈Z).
) (k∈Z).
求:(1)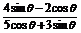 ;
;
(2)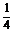 sin2
sin2 +
+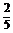 cos2
cos2 .
.
解:由已知得cos( +k
+k )≠0,
)≠0,
∴tan( +k
+k )=-2(k∈Z),即tan
)=-2(k∈Z),即tan =-2.
=-2.
(1)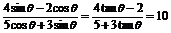 .
.
(2)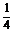 sin2
sin2 +
+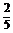 cos2
cos2 =
=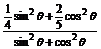 =
=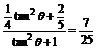 .
.
|
3.同角三角函数的关系式的基本用途:
根据一个角的某一个三角函数值,求出该角的其他三角函数值;化简同角三角函数式;证明同角的三角恒等式.
2.诱导公式:
|
|
-α |
π-α |
π+α |
2π-α |
2kπ+α |
|
sin |
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
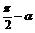 |
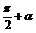 |
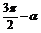 |
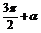 |
|
sin |
|
|
|
|
|
cos |
|
|
|
|
规律:奇变偶不变,符号看象限
1.同角公式:
(1) 平方关系:sin2α+cos2α=1,1+tan2α= ,1+cot2α=
(2) 商数关系:tanα= ,co tα=
tα=
(3) 倒数关系:tanα = 1,sinα =1,cotα =1
1,sinα =1,cotα =1
2.在计算或化简三角函数的关系式时,常常要对角 的范围以及相应的三角函数值的正负情况进行讨论,因此,在解答这类题时首先要弄清:①角的范围是什么?②对应的三角函数值是正还是负?③与此相关的定义、性质或公式有哪些?
的范围以及相应的三角函数值的正负情况进行讨论,因此,在解答这类题时首先要弄清:①角的范围是什么?②对应的三角函数值是正还是负?③与此相关的定义、性质或公式有哪些?
第2课时 同角三角函数的基本关系及诱导公式
|
1.本节内容是三角函数的基础内容,也是后续结论的根源所在,要求掌握好:如角度的范围、函数的定义、函数值的符号、函数值的大小关系及它们之间的相互转化关系.
13.三角函数线:在图中作出角 的正弦线、余弦线、正切线.
的正弦线、余弦线、正切线.
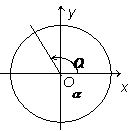
|
例1. 若 是第二象限的角,试分别确定2
是第二象限的角,试分别确定2 ,
, ,
,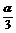 的终边所在位置.
的终边所在位置.
解: ∵ 是第二象限的角,
是第二象限的角,
∴k·360°+90°< <k·360°+180°(k∈Z).
<k·360°+180°(k∈Z).
(1)∵2k·360°+180°<2 <2k·360°+360°(k∈Z),
<2k·360°+360°(k∈Z),
∴2 是第三或第四象限的角,或角的终边在y轴的非正半轴上.
是第三或第四象限的角,或角的终边在y轴的非正半轴上.
(2)∵k·180°+45°< <k·180°+90°(k∈Z),
<k·180°+90°(k∈Z),
当k=2n(n∈Z)时,
n·360°+45°< <n·360°+90°;
<n·360°+90°;
当k=2n+1(n∈Z)时,
n·360°+225°< <n·360°+270°.
<n·360°+270°.
∴ 是第一或第三象限的角.
是第一或第三象限的角.
(3)∵k·120°+30°<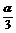 <k·120°+60°(k∈Z),
<k·120°+60°(k∈Z),
当k=3n(n∈Z)时,
n·360°+30°<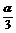 <n·360°+60°;
<n·360°+60°;
当k=3n+1(n∈Z)时,
n·360°+150°<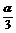 <n·360°+180°;
<n·360°+180°;
当k=3n+2(n∈Z)时,
n·360°+270°<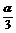 <n·360°+300°.
<n·360°+300°.
∴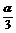 是第一或第二或第四象限的角.
是第一或第二或第四象限的角.
变式训练1:已知 是第三象限角,问
是第三象限角,问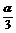 是哪个象限的角?
是哪个象限的角?
解: ∵ 是第三象限角,∴180°+k·360°<
是第三象限角,∴180°+k·360°< <270°+k·360°(k∈Z),
<270°+k·360°(k∈Z),
60°+k·120°<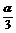 <90°+k·120°.
<90°+k·120°.
①当k=3m(m∈Z)时,可得
60°+m·360°<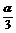 <90°+m·360°(m∈Z).
<90°+m·360°(m∈Z).
故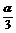 的终边在第一象限.
的终边在第一象限.
②当k=3m+1 (m∈Z)时,可得
180°+m·360°<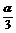 <210°+m·360°(m∈Z).
<210°+m·360°(m∈Z).
故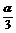 的终边在第三象限.
的终边在第三象限.
③当k=3m+2 (m∈Z)时,可得
300°+m·360°<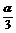 <330°+m·360°(m∈Z).
<330°+m·360°(m∈Z).
故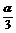 的终边在第四象限.
的终边在第四象限.
综上可知,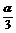 是第一、第三或第四象限的角.
是第一、第三或第四象限的角.
例2.
在单位圆中画出适合下列条件的角 的终边的范围,并由此写出角
的终边的范围,并由此写出角 的集合:
的集合:
(1)sin ≥
≥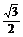 ;(2)cos
;(2)cos ≤
≤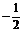 .
.
 解:(1)作直线y=
解:(1)作直线y=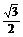 交单位圆于A、B两点,连结OA、OB,
交单位圆于A、B两点,连结OA、OB,
则OA与OB围成的区
域即为角 的终边的范围,故满足条件的角
的终边的范围,故满足条件的角 的集合为
的集合为

 |2k
|2k +
+ ≤
≤ ≤2k
≤2k +
+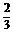
 ,k∈Z .
,k∈Z .
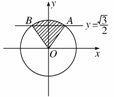
 (2)作直线x=
(2)作直线x=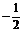 交单位圆于C、D两点,连结OC、OD,则OC与OD围成的区域(图中阴影部分)
交单位圆于C、D两点,连结OC、OD,则OC与OD围成的区域(图中阴影部分)
即为角 终边的范围.故满足条件的角
终边的范围.故满足条件的角 的集合为
的集合为
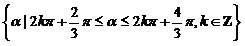 .
.
变式训练2:求下列函数的定义域:
(1)y=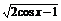 ;(2)y=lg(3-4sin2x).
;(2)y=lg(3-4sin2x).
解:(1)∵2cosx-1≥0,∴cosx≥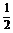 .
.
由三角函数线画出x满足条件的终边范围(如图阴影所示).
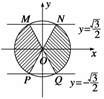 ∴x∈
∴x∈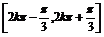 (k∈Z).
(k∈Z).
(2)∵3-4sin2x>0,∴sin2x<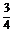 ,∴-
,∴-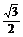 <sinx<
<sinx<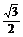 .
.
利用三角函数线画出x满足条件的终边范围(如右图阴影),
∴x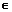 (k
(k -
- ,k
,k +
+ )(k
)(k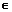 Z).
Z).
例3.
已知角 的终边在直线3x+4y=0上,求sin
的终边在直线3x+4y=0上,求sin ,cos
,cos ,tan
,tan 的值.
的值.
解:∵角 的终边在直线3x+4y=0上,
的终边在直线3x+4y=0上,
∴在角 的终边上任取一点P(4t,-3t) (t≠0),
的终边上任取一点P(4t,-3t) (t≠0),
则x=4t,y=-3t,
r=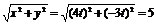 |t|,
|t|,
当t>0时,r=5t,
sin =
=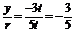 ,cos
,cos =
=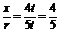 ,
,
tan =
=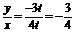 ;
;
当t<0时,r=-5t,sin =
=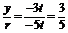 ,
,
cos =
=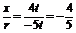 ,
,
tan =
=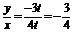 .
.
综上可知,t>0时,sin =
=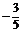 ,cos
,cos =
=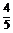 ,tan
,tan =
=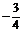 ;
;
t<0时,sin =
=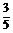 ,cos
,cos =-
=-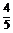 ,tan
,tan =
=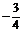 .
.
变式训练3:已知角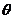 的终边经过点P
的终边经过点P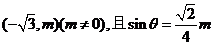 ,试判断角
,试判断角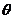 所在的象限,并求
所在的象限,并求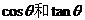 的值.
的值.
解:由题意,得 
故角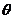 是第二或第三象限角.
是第二或第三象限角.
当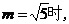
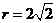 ,点P的坐标为
,点P的坐标为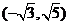 ,
,
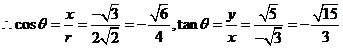
当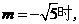
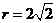 ,点P的坐标为
,点P的坐标为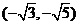 ,
,
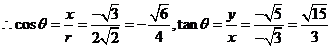
例4. 已知一扇形中心角为α,所在圆半径为R.
(1) 若α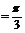 ,R=2cm,求扇形的弧长及该弧所在弓形面积;
,R=2cm,求扇形的弧长及该弧所在弓形面积;
(2) 若扇形周长为一定值C(C>0),当α为何值时,该扇形面积最大,并求此最大值.
解:(1)设弧长为l,弓形面积为S弓。
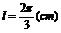
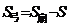 △=
△=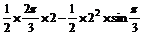
=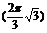 (cm2)
(cm2)
扇形周长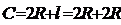 ∴
∴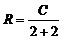
∴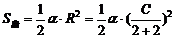
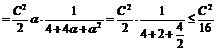
当且仅当22=4,即α=2时扇形面积最大为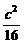 .
.
变式训练4:扇形OAB的面积是1cm2,它的周长是4cm,求中心角的弧度数和弦长AB.
解:设扇形的半径为r,弧长为l,中心角的弧度数为α
则有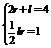 ∴
∴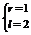
由|α|= 得α=2
∴|AB|=2·sin 1( cm )
得α=2
∴|AB|=2·sin 1( cm )
|
12、正弦、余弦、正切、余切函数的定义域和值域:
|
解析式 |
y=sinx |
y=cosx |
y=tanx |
|
定义域 |
|
|
|
|
值 域 |
|
|
|
10.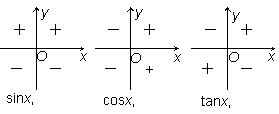 三角函数的符号与角所在象限的关系:
三角函数的符号与角所在象限的关系:
9.定义:设P(x, y)是角 终边上任意一点,且 |PO| =r,则sin
终边上任意一点,且 |PO| =r,则sin = ; cos
= ; cos = ;tan
= ;tan = ;
= ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com