2．y＝sinx，y＝cosx，y＝tanx的图象．

注：⑴ 正弦函数的对称中心为　　　　　　 ，对称轴为　　　　　　 ．

⑵ 余弦函数的对称中心为　　　　　　　 ，对称轴为　　　　　　 ．

⑶ 正切函数的对称中心为　　　 　　　．

1．用“五点法”作正弦、余弦函数的图象．

“五点法”作图实质上是选取函数的一个　　　　 ，将其四等分，分别找到图象的　　　　 点，　　　　 点及“平衡点”．由这五个点大致确定函数的位置与形状．

3．对于高次幂，往往采用三角公式降次，再依求证式的要求论证．

第7课时　　　 三角函数的图象与性质

2．条件等式的证明，注意认真观察，发现已知条件和求证等式之间的关系，选择适当的途径运用条件，从已知条件出发，以求证式为目标进行代数或三角恒等变形，逐步推出求证式．

1．证明三角恒等式的基本思路，是根据等式两端的特征通过三角恒等变换，应用化繁为简，左右归一，变更命题等方法使等式两端的“异”化为“同”．

2．三角条件等式的证明，关键在于仔细地找出所附加的条件和所要证明的结论之间的内在联系，其常用的方法有：

⑴ 代入法：就是将结论变形后将条件代入，从而转化为恒等式的证明．

⑵ 综合法：从条件出发逐步变形推出结论的方法．

⑶ 消去法：当已知条件中含有某些参数，而结论中不含这些参数，通过消去条件中这些参数达到证明等式的方法．

⑷ 分析法：从结论出发，逐步追溯到条件的证明方法，常在难于找到证题途径时用之．

例1．求证：＝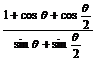

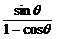
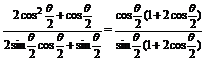
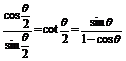证明：左边＝

＝＝右边

变式训练1：求证：tan(α+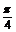)+tan(α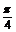－)＝2tan2α

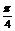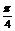证明：∵(α+)+(α－)＝2α

∴tan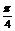[(α+)+(α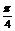－)]＝tan2α

∴

∴

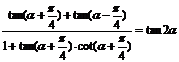
∴tan(α+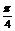)+tan(α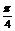－)＝2tan2α

例2．求证：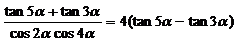

证明：左边＝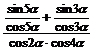

＝

＝

＝

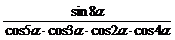
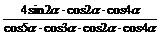
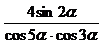
右边＝4()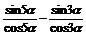

＝4·＝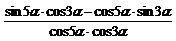

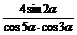
∴左边＝右边　 即等式成立

变式训练2：已知2tanA＝3tanB，求证：tan(A－B)＝．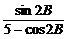

证明：tan(A－B)＝

＝

＝

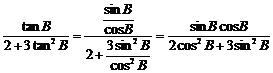
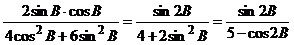
例3．如图所示，D是直线三角形△ABC斜边上BC上一点，AB＝AD，记∠CAD=α，∠ABC=β．

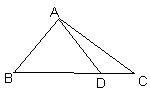(1)证明：sinα+cos2β=0；

(2)若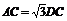，求β的值．

解：(1)∵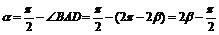

∴

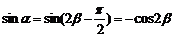
即sinα+cos2β＝0

(2)在△ADC中，由正弦定理得．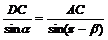

即　　 ∴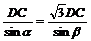

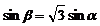
由(1)sinα＝－cos2β

∴

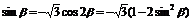
即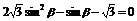

解得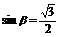或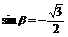_{[来源:学,科,网Z,X,X,K]}

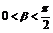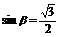因为，所以从而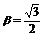

变式训练3.已知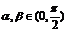且sinβ·cosα＝cos(α+β)．

(1)求证：；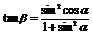

(2)用tanβ表示tanα．

解：(1)∵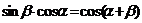

∴

∴

∴

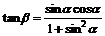
(2)

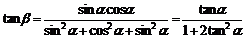
例4.在△ABC中，若sinA·cos²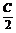+sinC·cos²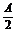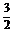＝sinB，求证：sinA+sinC＝2 sinB．

证明：∵sinA·cos²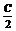+sinC·cos²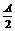＝sinB

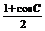∴sinA·+sinC·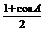＝sinB

∴sinA+sinC+sinA·cosC+cosA·sinC＝3sinB

∴sinA+sinC+sin(A+C)＝3sinB

∵sin(A+C)＝sinB　 ∴sinA+sinC＝2sinB

变式训练4：已知sinθ+cosθ＝2sinα，sinθ·cosθ＝sin²β，求证：2cos2α＝cos2β．

证明：(sinθ+cosθ)²

＝1+2sinθ·cosθ＝4sin²α

将sinθ·cosθ＝sin²β代入得1+2sin²β＝4sin²α

∴1+1－cos2β＝2(1－cos2α)

∴2cos2α＝cos2β

1．三角条件等式的证明就是逐步将条件等价转化为结论等式的过程，须注意转化过程确保充分性成立．

3．证明三角恒等式的基本方法有：⑴ 化繁为简；⑵ 左右归一；⑶ 变更问题．

2．证三角恒等式的基本思路是“消去差异，促成同一”，即通过观察、分析，找出等式两边在角、名称、结构上的差异，再选用适当的公式，消去差异，促进同一．

1．三角恒等式的证明实质是通过恒等变形，消除三角恒等式两端结构上的差异(如角的差异、函数名称的差异等)．