
4.函数y=Asin(ωx+ )(A>0,ω>0)的单调区间的确定的基本思想是把(ωx+
)(A>0,ω>0)的单调区间的确定的基本思想是把(ωx+ )看作一个整体,再利用正弦函数的单调区间解出x即为所求.若ω<0,可用诱导公式变为y=-Asin(-ωx-
)看作一个整体,再利用正弦函数的单调区间解出x即为所求.若ω<0,可用诱导公式变为y=-Asin(-ωx- )再仿照以上方法解之.
)再仿照以上方法解之.
|
3.求周期一般先将函数式化为y=Af(ωx+ )(f为三角函数),再用周期公式求解.
)(f为三角函数),再用周期公式求解.
2.求函数值域的问题一方面要熟悉求值域的一般方法和依据,另一方面要注意三角函数的有界性.
1.求三角函数的定义域既要注意一般函数求定义域的规律,又要注意三角函数本身的特有属性,如常常丢掉使tanx有意义的x≠nπ+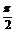 (n∈Z).
(n∈Z).
2.函数y=sinx的对称性与周期性的关系.
⑴ 若相邻两条对称轴为x=a和x=b,则T= .
⑵ 若相邻两对称点(a,0)和(b,0) ,则T= .
⑶ 若有一个对称点(a,0)和它相邻的一条对称轴x=b,则T= .
注:该结论可以推广到其它任一函数.
|
例1. 化简f (x)=cos(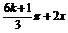 )+cos(
)+cos(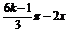 )+2
)+2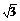 sin(
sin( +2x)(x∈R,k∈Z).并求f (x)的值域和最小正周期.
+2x)(x∈R,k∈Z).并求f (x)的值域和最小正周期.
解:(1) f(x) =2sin(ax+ )(0<a<1)
)(0<a<1)
由于f(x)·g(x)最小正周期相同
得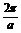 =
=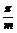 即a=2m
即a=2m
又f(1)=2g(1) 即2sin(a+ )=2tan(m+
)=2tan(m+ )
)
把a=2m代入得sin(2m+ )=tan(m+
)=tan(m+ )
)
∴2sin(m+ )cos(m+
)cos(m+ )=
)=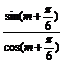
∴sin(m+ )=0或cos(m+
)=0或cos(m+ )=±
)=±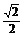
当sin(m+ )=0时,m=k
)=0时,m=k -
- (k≠z),这与0<m<1矛盾.
(k≠z),这与0<m<1矛盾.
当cos(m+ )=±
)=±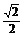 时,m=k
时,m=k +
+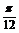 或m=k
或m=k -
-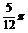 (k∈z),现由0<m<1时得m=
(k∈z),现由0<m<1时得m=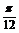 故a=
故a=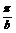
∴f(x)=2sin( x+
x+ ),g(x)=tan(
),g(x)=tan(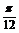 x+
x+ )
)
(2) 由2k -
-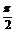 ≤
≤ x+
x+ ≤2k
≤2k +
+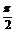 得
得
x∈[12k-5,12k+1]
∴f(x)的单调递增区间为[12k-5,12k+1] (k∈z)
变式训练1:已知函数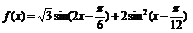
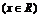 ;
;
(1)求函数f(x)的最小正周期;
(2)求使函数f(x)取得最大值的x的集合.
解:(1)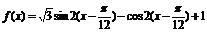
=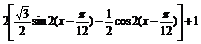
=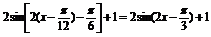
∴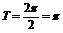
(2)当f(x)取最大值时,sin(2x- )=1
)=1
有2x- =2k
=2k +
+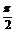 即x=k
即x=k +
+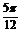 (k∈z)
(k∈z)
故所求x的集合为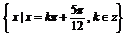
例2已知函数f (x)=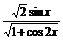
⑴ 求f (x)的定义域.
⑵ 用定义判断f (x)的奇偶性.
⑶ 在[-π,π]上作出函数f (x)的图象.
⑷ 指出f (x)的最小正周期及单调递增区间.
解:(1) 由1+cos2x>0得2cos2x>0
∴cosx≠0即x≠kπ+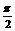 ,(k∈z)
,(k∈z)
∴函数f (x)的定义域为{x|x≠kπ+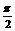 ,k∈z|}
,k∈z|}
(2)∵定义域关于原点对称,且对任意的定义域中x,
f (-x)=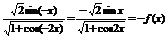
∴f (x)为奇函数.
 (3) f (x)=
(3) f (x)=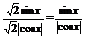 又x∈[-π,π]
又x∈[-π,π]
且x≠-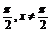
∴f(x)=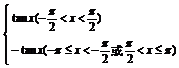
f (x)的图象如右:
(4) 由图知,f(x)的最小正周期为2π.
f (x)的单调递增区间是( )(k∈z)
)(k∈z)
 变式训练2:求下列函数的定义域:
变式训练2:求下列函数的定义域:
(1)y=lgsin(cosx);(2)y=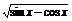 .
.
解 (1)要使函数有意义,必须使sin(cosx)>0.
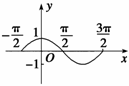
 ∵-1≤cosx≤1,∴0<cosx≤1.
∵-1≤cosx≤1,∴0<cosx≤1.
方法一 利用余弦函数的简图得知定义域为{x|-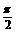 +2k
+2k <x<
<x<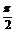 +2k
+2k ,k∈Z}.
,k∈Z}.
方法二 利用单位圆中的余弦线OM,依题意知0<OM≤1,
∴OM只能在x轴的正半轴上,
∴其定义域为
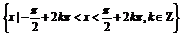 .
.
(2)要使函数有意义,必须使sinx-cosx≥0.
方法一 利用图象.在同一坐标系中画出[0,2 ]上y=sinx和y=cosx的图象,如图所示.
]上y=sinx和y=cosx的图象,如图所示.
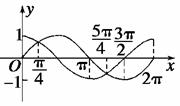
在[0,2 ]内,满足sinx=cosx的x为
]内,满足sinx=cosx的x为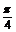 ,
,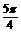 ,再结合正弦、余弦函数的周期是2
,再结合正弦、余弦函数的周期是2 ,
,
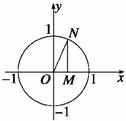 所以定义域为
所以定义域为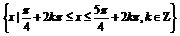 .
.
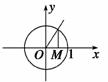
方法二 利用三角函数线,
如图MN为正弦线,OM为余弦线,
要使sinx≥cosx,即MN≥OM,
则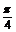 ≤x≤
≤x≤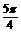 (在[0,2
(在[0,2 ]内).
]内).
∴定义域为
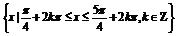 .
.
方法三 sinx-cosx= sin
sin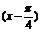 ≥0,
≥0,
将x-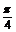 视为一个整体,由正弦函数y=sinx的图象和性质
视为一个整体,由正弦函数y=sinx的图象和性质
可知2k ≤x-
≤x-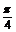 ≤
≤ +2k
+2k ,
,
解得2k +
+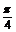 ≤x≤
≤x≤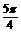 +2k
+2k ,k∈Z.
,k∈Z.
所以定义域为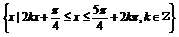 .
.
例3设函数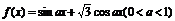 ,
,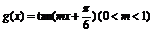 ,已知f(x)、g(x)的最小正周期相同,且2(g)=f(1);
,已知f(x)、g(x)的最小正周期相同,且2(g)=f(1);
(1)试确定f(x)、g(x)的解的式;
(2)求函数f(x)的单调递增区间.
解:(1)当a=1时,f(x)=2cos2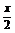 +sinx+b
+sinx+b
=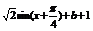
∴递增区间为[2kπ-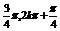 ](k∈z)
](k∈z)
(2)∵f (x)=a(sinx+cosx)+a+b=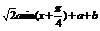
而x∈[0,π],x+ ∈[
∈[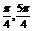 ]
]
∴sin(x+ )∈[
)∈[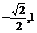 ]
]
∴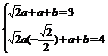 ∴
∴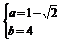
变式训练3:已知函数f (x)=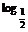 (sinx-cosx)
(sinx-cosx)
⑴ 求它的定义域和值域;
⑵ 求它的单调区间;
⑶ 判断它的奇偶性;
⑷ 判定它的周期性,如果是周期函数,求出它的最小正周期.
解:(1) 由题意得:si nx-cosx>0即
nx-cosx>0即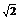 sin(x-
sin(x-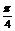 )>0
)>0
从而得2kπ+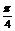 <x<2kπ+
<x<2kπ+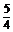 π
π
函数的定义域为(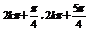 )(k∈z)
)(k∈z)
∵0<sin(x-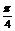 )≤1 ∴0<sinx-cosx≤
)≤1 ∴0<sinx-cosx≤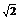
即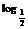 (sinx-cosx)≥
(sinx-cosx)≥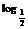
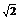 =-
=-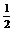 故函数f (x)的值域为[-
故函数f (x)的值域为[-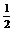 ,+∞]
,+∞]
(2) ∵sinx-cosx=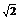 sin(x-
sin(x-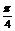 )在f(x)的定义域上的单调递增区间为(
)在f(x)的定义域上的单调递增区间为(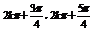 )(k∈z),单调递减区间为[
)(k∈z),单调递减区间为[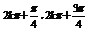 ](k∈z)
](k∈z)
(3) ∵f(x)的定义域在数轴上对应的点关于原点不对称.
∴f(x)是非奇非偶函数.
(4) ∵f(x+2π)=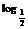 [sin(x+2π)-cos(x+2π)]
[sin(x+2π)-cos(x+2π)]
=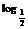 (sinx-cosx)=f(x)
(sinx-cosx)=f(x)
∴f (x)函数的最小正周期T=2π
例4.已知函数y=acosx+b的最大值为1,最小值是-3,试确定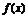 =b sin(ax+
=b sin(ax+ )的单调区间.
)的单调区间.
解:(1)若a>0,则a+b=1,-a+b=-3,
∴ a=2,b=-1,此时,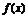 =-sin(2x+
=-sin(2x+ )
)
单调增区间为[kπ+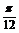 ,kπ+
,kπ+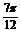 ] (k∈z)
] (k∈z)
单调减区间为[kπ-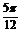 ,kπ+
,kπ+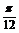 ] (k∈z)
] (k∈z)
(2) 若a<0,则-a+b=1,a+b=-3,
∴ a=-2,b=-1,
单调增区间为[kπ-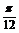 ,kπ+
,kπ+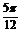 ] (k∈z)
] (k∈z)
单调减区间为[kπ+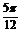 ,kπ+
,kπ+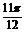 ] (k∈z)
] (k∈z)
变式训练4:某港口水的深度y(米)是时间t(0≤t<24,单位:时)的函数,记作y=f(t),下面是某日水深的数据:
|
t(时) |
0 |
3 |
6 |
9 |
12 |
|
y(米) |
10 |
13 |
9.9 |
7 |
10 |
|
t(时) |
15 |
18 |
21 |
24 |
|
|
y(米) |
13 |
10.1 |
7 |
10 |
|
经过长期观察,y=f(t)的曲线可以近似地看成函数y=Asinωx+b的图象.
(1)试根据以上数据,求出函数y=f(t)的近似表达式;
(2)一般情况下,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底中需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米,如果希望该船在一天内安全进出港,请问,它至多在港里停留多长时间(忽略进出港所需的时间)?
解:(1) 由已知数据,易知函数y=f(t)的周期T=12,振幅A=3,b=10
∴y=3sin t=10
t=10
(2) 由题意,该船进出港时,水深应不小于5+6.5=11.5(米)
∴3sin t+10≥11.5 sin
t+10≥11.5 sin t≥
t≥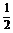
解得2k +
+ ≤
≤ t≤2k
t≤2k +
+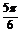
即12k+1≤t≤12k+5 k∈z
在同一天内,取k=0或1.
∴1≤t≤5 或 13≤t≤17
∴该船最早能在凌晨1时进港,最迟下午17时出港,在港内最多能停留16小时.
|
1.三角函数的性质
|
函
数 |
y=sinx |
y=cosx |
y=tanx |
|
定义域 |
|
|
|
|
值
域 |
|
|
|
|
奇偶性 |
|
|
|
|
有界性 |
|
|
|
|
周期性 |
|
|
|
|
单调性 |
|
|
|
|
最大(小)值 |
|
|
|
2.给出图象求解析式y=Asin(ωx+ )+B的难点在于ω、
)+B的难点在于ω、 的确定,本质为待定系数法,基本方法是:⑴ “五点法”运用“五点”中的一点确定.
的确定,本质为待定系数法,基本方法是:⑴ “五点法”运用“五点”中的一点确定.
⑵ 图像变换法,即已知图象是由哪个函数的图象经过变换得到的,通常可由零点或最值点确定T→ω.
第8课时 三角函数的性质
|
1.图象变换的两种途径
⑴ 先相位变换后周期变换
y=sinx  y=sin(x+
y=sin(x+ )
) y=sin(ωx+
y=sin(ωx+ )
)
⑵ 先周期变换后相位变换
y=sinx  y=sinωx
y=sinωx y=sinω (x+
y=sinω (x+ )
)
4.函数y=Asin(ωx+ )的图象与函数y=sinx的图象关系.
)的图象与函数y=sinx的图象关系.
振幅变换:y=Asinx(A>0,A≠1)的图象,可以看做是y=sinx的图象上所有点的纵坐标都 ,(A>1)或 (0<A<1)到原来的 倍(横坐标不变)而得到的.
周期变换:y=sinωx(ω>0,ω≠1)的图象,可以看做是把y=sinx的图象上各点的横坐标 (ω>1)或 (0<ω<1)到原来的 倍(纵坐标不变)而得到的.由于y=sinx周期为2π,故y=sinωx(ω>0)的周期为 .
相位变换:y=sin(x+ )(
)( ≠0)的图象,可以看做是把y=sinx的图象上各点向 (
≠0)的图象,可以看做是把y=sinx的图象上各点向 ( >0)或向 (
>0)或向 ( <0)平移 个单位而得到的.
<0)平移 个单位而得到的.
由y=sinx的图象得到y=Asin(ωx+ )的图象主要有下列两种方法:
)的图象主要有下列两种方法:
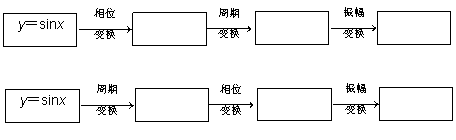
或
说明:前一种方法第一步相位变换是向左( >0)或向右(
>0)或向右( <0)平移 个单位.后一种方法第二步相位变换是向左(
<0)平移 个单位.后一种方法第二步相位变换是向左( >0)或向右(
>0)或向右( <0)平移 个单位.
<0)平移 个单位.
例1.已知函数y=Asin(ωx+ )(A>0,ω>0)
)(A>0,ω>0)
⑴ 若A=3,ω=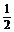 ,
, =-
=- ,作出函数在一个周期内的简图.
,作出函数在一个周期内的简图.
⑵ 若y表示一个振动量,其振动频率是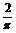 ,当x=
,当x=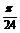 时,相位是
时,相位是 ,求ω和
,求ω和 .
.
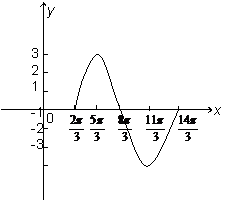 解:(1) y=3sin(
解:(1) y=3sin(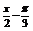 )列表(略)图象如下:
)列表(略)图象如下:
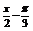 |
0 |
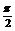 |
π |
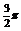 |
2π |
|
x |
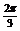 |
 |
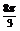 |
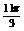 |
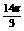 |
|
y |
0 |
3 |
0 |
-3 |
0 |
(2)依题意有:
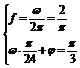 ∴
∴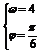
变式训练1:已知函数y=2sin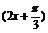 ,
,
(1)求它的振幅、周期、初相;
(2)用“五点法”作出它在一个周期内的图象;
(3)说明y=2sin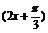 的图象可由y=sinx的图象经过怎样的变换而得到.
的图象可由y=sinx的图象经过怎样的变换而得到.
解 (1)y=2sin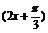 的振幅A=2,周期T=
的振幅A=2,周期T=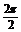 =
= ,初相
,初相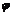 =
= .
.
(2)令X=2x+ ,则y=2sin
,则y=2sin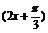 =2sinX.
=2sinX.
列表,并描点画出图象:
|
x |
- |
 |
 |
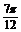 |
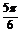 |
|
X |
0 |
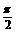 |
 |
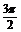 |
2 |
|
y=sinX |
0 |
1 |
0 |
-1 |
0 |
y=2sin(2x+ ) ) |
0 |
2 |
0 |
-2 |
0 |
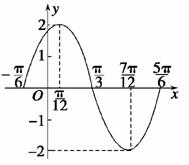
(3)方法一
把y=sinx的图象上所有的点向左平移 个单位,得到y=sin
个单位,得到y=sin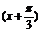 的图象,再把y=sin
的图象,再把y=sin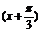 的图象上的点的横坐标缩短到原来的
的图象上的点的横坐标缩短到原来的 倍(纵坐标不变),得到y=sin
倍(纵坐标不变),得到y=sin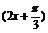 的图象,最后把y=sin
的图象,最后把y=sin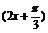 上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin
上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin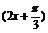 的图象.
的图象.
方法二 将y=sinx的图象上每一点的横坐标x缩短为原来的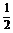 倍,纵坐标不变,得到y=sin2x的图象;
倍,纵坐标不变,得到y=sin2x的图象;
再将y=sin2x的图象向左平移 个单位;
个单位;
得到y=sin2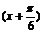 =sin
=sin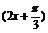 的图象;再将y=sin
的图象;再将y=sin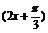 的图象上每一点的横坐标保持不变,纵坐标伸长为原来的2倍,得到y=2sin
的图象上每一点的横坐标保持不变,纵坐标伸长为原来的2倍,得到y=2sin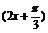 的图象.
的图象.
例2已知函数y=3sin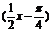
(1)用五点法作出函数的图象;
(2)说明此图象是由y=sinx的图象经过怎么样的变化得到的;
(3)求此函数的振幅、周期和初相;
(4)求此函数图象的对称轴方程、对称中心.
解 (1)列表:
|
x |
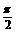 |
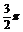 |
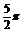 |
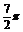 |
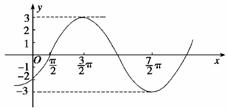 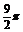 |
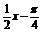 |
0 |
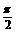 |
 |
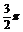 |
2 |
3sin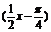 |
0 |
3 |
0 |
-3 |
0 |
描点、连线,如图所示:
(2)方法一 “先平移,后伸缩”.
先把y=sinx的图象上所有点向右平移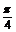 个单位,得到y=sin
个单位,得到y=sin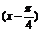 的图象;再把y=sin
的图象;再把y=sin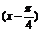 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到
y=sin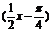 的图象,最后将y=sin
的图象,最后将y=sin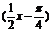 的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin
的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin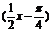 的图象.
的图象.
方法二 “先伸缩,后平移”
先把y=sinx的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到y=sin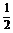 x的图象;再把y=sin
x的图象;再把y=sin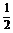 x图象上所有的点向右平移
x图象上所有的点向右平移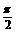 个单位,
个单位,
得到y=sin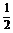 (x-
(x-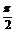 )=sin
)=sin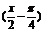 的图象,最后将y=sin
的图象,最后将y=sin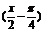 的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin
的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin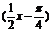 的图象.
的图象.
(3)周期T= =
=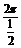 =4
=4 ,振幅A=3,初相是-
,振幅A=3,初相是-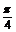 .
.
(4)令 =
=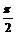 +k
+k (k∈Z),
(k∈Z),
得x=2k +
+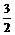
 (k∈Z),此为对称轴方程.
(k∈Z),此为对称轴方程.
令 x-
x-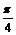 =k
=k (k∈Z)得x=
(k∈Z)得x=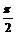 +2k
+2k (k∈Z).
(k∈Z).
对称中心为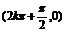 (k∈Z).
(k∈Z).
变式训练2:已知函数
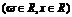 的最小正周期为π且图象关于
的最小正周期为π且图象关于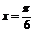 对称;
对称;
(1) 求f(x)的解析式;
(2) 若函数y=1-f(x)的图象与直线y=a在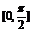 上中有一个交点,求实数a的范围.
上中有一个交点,求实数a的范围.
解:(1)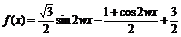
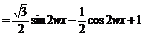
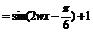
∵w∈R 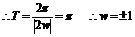
当w=1时,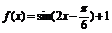 此时
此时 不是它的对称轴
不是它的对称轴
∴w=-1 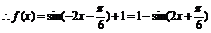
(2)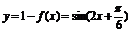
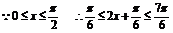
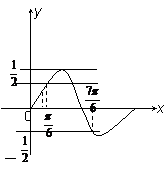 如图:∵直线y=a在
如图:∵直线y=a在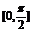 上与y=1-f(x)图象只有一个交点
∴
上与y=1-f(x)图象只有一个交点
∴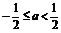 或a=1
或a=1
例3.如图为y=Asin(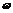 x+
x+ )的图象的一段,求其解析式.
)的图象的一段,求其解析式.
 解
方法一 以N为第一个零点,
解
方法一 以N为第一个零点,
则A=-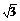 ,T=2
,T=2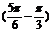 =
= ,
,
∴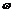 =2,此时解析式为y=-
=2,此时解析式为y=-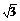 sin(2x+
sin(2x+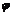 ).
).
∵点N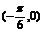 ,∴-
,∴- ×2+
×2+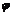 =0,∴
=0,∴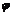 =
= ,
,
所求解析式为y=-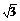 sin
sin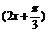 . ①
. ①
方法二 由图象知A=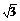 ,
,
以M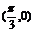 为第一个零点,P
为第一个零点,P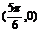 为第二个零点.
为第二个零点.
列方程组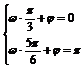 解之得
解之得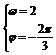 .
.
∴所求解析式为y=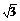 sin
sin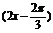 . ②
. ②
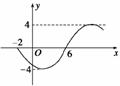 变式训练3:函数y=Asin(
变式训练3:函数y=Asin(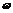 x+
x+ )(
)(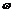 >0,|
>0,| |<
|< 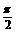 ,x∈R)的部分图象如图,则函数表达式为( )
,x∈R)的部分图象如图,则函数表达式为( )
A. y=-4sin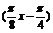 B. y=-4sin
B. y=-4sin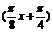
C. y=4sin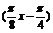 D. y=4sin
D. y=4sin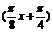
答案 B
例4.设关于x的方程cos2x+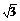 sin2x=k+1在[0,
sin2x=k+1在[0,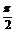 ]内有两不同根α,β,求α+β的值及k的取值范围.
]内有两不同根α,β,求α+β的值及k的取值范围.
解:由cos2x+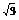 sin2x=k+1得 2sin(2x+
sin2x=k+1得 2sin(2x+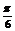 )=k+1
)=k+1
即sin(2x+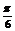 )=
)=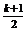
设c: y=sin(2x+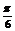 ),l: y=
),l: y=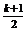 ,在同一坐标系中作出它们的图象(略)
,在同一坐标系中作出它们的图象(略)
由图易知当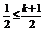 <1时, 即0≤k<1时
<1时, 即0≤k<1时
直线l与曲线c有两个交点,且两交点的横坐标为α、β,从图象中还可以看出α、β关于x=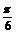 对称.。故α+β=
对称.。故α+β=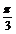
变式训练4.已知函数f (x)=sin(ωx+ )(ω>0,0≤
)(ω>0,0≤ ≤π)是R上的偶函数,其图象关于点M(
≤π)是R上的偶函数,其图象关于点M(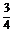 π,0)对称,且在区间[0,
π,0)对称,且在区间[0,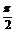 ]上是单调函数,求
]上是单调函数,求 和ω的值.
和ω的值.
解:由f (x)是偶函数,得f(-x)=f (x)即sin(-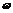 x+
x+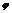 )=sin(
)=sin(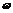 x+
x+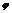 )
)
∴-cos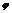 sin
sin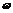 x=cos
x=cos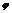 sin
sin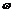 x对任意x都成立,且
x对任意x都成立,且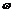 >0, cos
>0, cos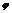 =0
=0
依题意设0≤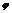 ≤π ∴
≤π ∴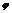 =
=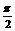
由f(x)的图象关于点M对称,
得f(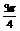 -x)=-f (
-x)=-f (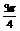 +x)
+x)
取x=0得f (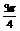 )=-f (
)=-f (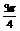 ) f (
) f (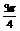 )=0
)=0
∴f(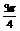 )=sin(
)=sin(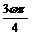 +
+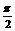 )=cos
)=cos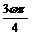 =0
=0
又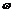 >0得
>0得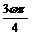 =
=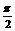 +kπ
+kπ
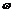 =
=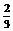 (2k+1) (k=0,1,2……)
(2k+1) (k=0,1,2……)
当k=0时,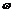 =
=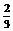 f
(x)=sin(
f
(x)=sin(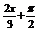 )在[0,
)在[0,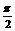 ]上是减函数;
]上是减函数;
当k=1时,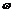 =2 f (x)=sin(2x+
=2 f (x)=sin(2x+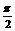 )在[0,
)在[0,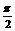 ]上是减函数;
]上是减函数;
当k≥2时,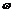 ≥
≥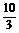 f (x)=sin(
f (x)=sin(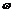 x
x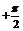 )在[0,
)在[0,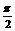 ]上不是减函数;
]上不是减函数;
∴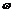 =
=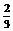 或
或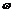 =2
=2
|
|||
|
|||
3.“五点法”作y=Asin(ωx+ )(ω>0)的图象.
)(ω>0)的图象.
令x'=ωx+ 转化为y=sinx',作图象用五点法,通过列表、描点后作图象.
转化为y=sinx',作图象用五点法,通过列表、描点后作图象.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com