
3. 已知α、β均为锐角,若P:sinα<sin(α+β),q:α+β<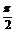 ,则P是q的( )
,则P是q的( )
A.充分而不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2. 若 ,则2x与3sinx的大小关系是 ( )
,则2x与3sinx的大小关系是 ( )
A.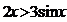 B.
B.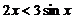
C. D.与x的取值有关
D.与x的取值有关
1. 已知sinθ=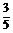 ,sin2θ<0,则tanθ等于 ( )
,sin2θ<0,则tanθ等于 ( )
A.-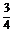 B.
B.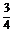
C.-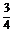 或
或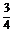 D.
D.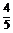
4.含参数函数的最值,解题要注意参数的作用.
三角函数章节测试题
3.求三角函数的最值时,一般要进行一些三角变换以及代数换元,须注意函数有意义的条件和弦函数的有界性.
2.三角函数的最值都是在给定区间上取得的.因而特别要注意题设所给出的区间.
1.求三角函数最值的方法有:① 配方法;②化为一个角的三角函数;③ 数形结合;④ 换元法;⑤ 基本不等式法.
3.二分法求方程的近似解
二分法求方程的近似解,首先要找到方程的根所在的区间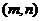 ,则必有
,则必有 ,再取区间的中点
,再取区间的中点 ,再判断
,再判断 的正负号,若
的正负号,若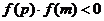 ,则根在区间
,则根在区间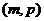 中;若
中;若 ,则根在
,则根在 中;若
中;若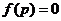 ,则
,则 即为方程的根.按照以上方法重复进行下去,直到区间的两个端点的近似值相同(且都符合精确度要求),即可得一个近似值.
即为方程的根.按照以上方法重复进行下去,直到区间的两个端点的近似值相同(且都符合精确度要求),即可得一个近似值.
|
例1. 求下列函数的最值.
⑴ y=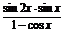 ;
;
⑵ y=2 cos( +x)+2cosx;
+x)+2cosx;
⑶  .
.
解:(1) y=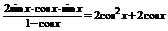
=
∴ 当cosx= 时,ymin=
时,ymin=
∵ cosx≠1
∴ 函数y没有最大值。
(2) y=2cos( )+2cosx
)+2cosx
=2cos
=3cosx-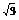 sinx
sinx
=2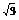 cos(
cos(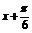 )
)
∴当cos(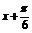 )=-1时,ymin=-
)=-1时,ymin=-
当cos(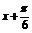 )=1时,ymax=
)=1时,ymax=
(3)
由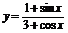 得sinx-ycosx=3y-1
得sinx-ycosx=3y-1
∴ =3y-1 (tan
=3y-1 (tan =-y)
=-y)
∵|sin(x+ )|≤1 ∴|3y-1|≤
)|≤1 ∴|3y-1|≤
解得0≤y≤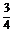 故
故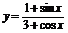 的值域为[0,
的值域为[0,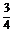 ]
]
注:此题也可用其几何意义在求值域.
变式训练1:求下列函数的值域:
(1)y= ;
;
(2)y=sinx+cosx+sinxcosx;
(3)y=2cos +2cosx.
+2cosx.
解 (1)y= =
=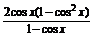
=2cos2x+2cosx=2 -
-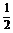 .
.
于是当且仅当cosx=1时取得ymax=4,但cosx≠1,
∴y<4,且ymin=-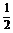 ,当且仅当cosx=-
,当且仅当cosx=-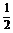 时取得.
时取得.
故函数值域为 .
.
(2)令t=sinx+cosx,则有t2=1+2sinxcosx,
即sinxcosx= .
.
有y=f(t)=t+ =
= .
.
又t=sinx+cosx= sin
sin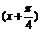 ,
,
∴- ≤t≤
≤t≤ .
.
故y=f(t)=  (-
(- ≤t≤
≤t≤ ),
),
从而知:f(-1)≤y≤f( ),即-1≤y≤
),即-1≤y≤ +
+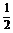 .
.
即函数的值域为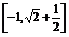 .
.
(3)y=2cos +2cosx
+2cosx
=2cos cosx-2sin
cosx-2sin sinx+2cosx
sinx+2cosx
=3cosx-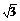 sinx
sinx
=2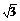
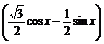
=2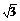 cos
cos .
.
∵ ≤1
≤1
∴该函数值域为[-2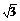 ,2
,2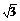 ].
].
例2. 试求函数y=sinx+cosx+2sinxcosx+2的最大值与最小值,又若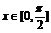 呢?
呢?
解: 令t=sinx+cosx 则t∈[- ,
, ]
]
又2sinx+cosx=(sinx+cosx)2-1=t2-1
∴y=t2+t+1=(t+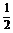 )2+
)2+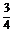 ,显然ymax=3+
,显然ymax=3+
若x∈[0,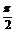 ] 则t∈[1,
] 则t∈[1, ]
]
y=(t+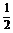 )+
)+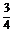 在[1,
在[1, ]单调递增.
]单调递增.
当t=1即x=0或x=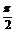 时,y取最小值3.
时,y取最小值3.
当t= 即x=
即x=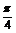 时,y取最大值3+
时,y取最大值3+ .
.
变式训练2:求函数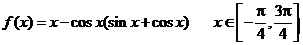 的最大值和最小值.
的最大值和最小值.
点拔:三角函数求最值一般利用三角变形求解,此题用常规方法非常困难,而用导数求最值既方便又简单.
解:f(x)=x-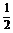 (sin2x+cos2x)-
(sin2x+cos2x)-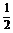
∴f´(x)=1+ sin(2x-
sin(2x-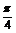 )
)
∵x∈[-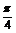 ,
,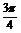 ]
∴2x-
]
∴2x-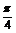 ∈[-
∈[-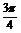 ,
, ]
]
令f´(x)=0 得sin(2x-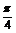 )=-
)=-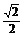
∴x=0,-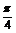 ,
,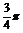
∵f(0)=-1,而f(-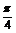 )=-
)=-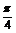 f(
f(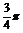 )=
)=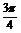
∴当x=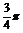 时,[f(x)]max=
时,[f(x)]max=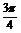
当x=0时,[f(x)]min=-1
例3. 已知sinx+siny=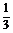 ,求siny-cos2x的最大值.
,求siny-cos2x的最大值.
解:∵sinx+siny= ∴siny=
∴siny=
∴siny-cos2x= -(1-sin2x)
-(1-sin2x)
=
=
又∵-1≤siny≤1
∴ 而-1≤sinx≤1
而-1≤sinx≤1
∴ ≤sinx≤1
≤sinx≤1
∴当sinx= 时,siny-cos2x取得最大值
时,siny-cos2x取得最大值 。
。
变式训练3:在△ABC中,角A、B、C的对边分别为a、b、c,若b2=ac,求y= 的取值范围.
的取值范围.
解:y=
又cosB= ≥
≥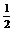
∴ 0<B≤ ∴
∴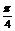 <B+
<B+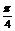 ≤
≤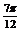
∴ 1<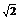 sin(B+
sin(B+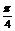 )≤
)≤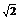 [来源:Z&xx&]
[来源:Z&xx&]
即1<y≤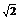
例4.设a≥0,若y=cos2x-asinx+b的最大值为0,最小值为-4,试求a与b的值,并求出使y取得最大、最小值时的x值.
解:原函数变形为
y=-
∵-1≤sinx≤1,a≥0
∴若0≤a≤2,当sinx=- 时
时
ymax=1+b+ =0 ①
=0 ①
当sinx=1时,ymin=-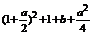
=-a+b=-4 ②
联立①②式解得a=2,b=-2
y取得最大、小值时的x值分别为:
x=2kπ-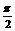 (k∈Z),x=2kπ+
(k∈Z),x=2kπ+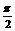 (k∈Z)
(k∈Z)
若a>2时, ∈(1,+∞)
∈(1,+∞)
∴ymax=- =0 ③
=0 ③
ymin=- ④
④
由③④得a=2时,而 =1 (1,+∞)舍去.
=1 (1,+∞)舍去.
故只有一组解a=2,b=-2.
变式训练4:设函数 (其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为 .
.
(1)求ω的值;
(2)如果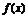 在区间
在区间 的最小值为
的最小值为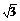 ,求a的值.
,求a的值.
解:(1)
f(x)=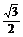 cos
cos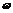 x+
x+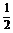 sin2
sin2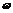 x+
x+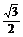 +a
+a
=sin(2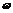 x+
x+ )+
)+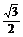 +a
+a
依题意得2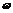 ·
· +
+ =
=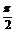 解得
解得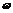 =
=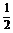
(2)
由(1)知f(x)=sin(2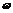 x+
x+ )+
)+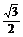 +a
+a
又当x∈ 时,x+
时,x+ ∈
∈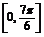
故-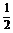 ≤sin(x+
≤sin(x+ )≤1
)≤1
从而f(x)在 上取得最小值-
上取得最小值-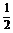 +
+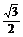 +a
+a
|
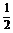 +
+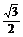 +a=
+a=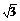 故a=
故a=
2.函数与方程
两个函数 与
与 图象交点的横坐标就是方程
图象交点的横坐标就是方程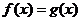 的解;反之,要求方程
的解;反之,要求方程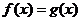 的解,也只要求函数
的解,也只要求函数 与
与 图象交点的横坐标.
图象交点的横坐标.
1.一元二次函数与一元二次方程
一元二次函数与一元二次方程(以后还将学习一元二次不等式)的关系一直是高中数学函数这部分内容中的重点,也是高考必考的知识点.我们要弄清楚它们之间的对应关系:一元二次函数的图象与 轴的交点的横坐标是对应一元二次方程的解;反之,一元二次方程的解也是对应的一元二次函数的图象与
轴的交点的横坐标是对应一元二次方程的解;反之,一元二次方程的解也是对应的一元二次函数的图象与 轴的交点的横坐标.
轴的交点的横坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com