
18.(本题14分)
(Ⅰ) ,其最小正周期是
,其最小正周期是 ,
,
又当 ,即
,即 时,
时, 取得最小值
取得最小值 ,
,
所以函数 的最小值是
的最小值是 ,此时
,此时 的集合为
的集合为 . 6分
. 6分
(Ⅱ)
由 ,得
,得 ,则
,则 ,
,
 ,
,
若 对于
对于 恒成立,则
恒成立,则 8分
8分
11. 90° 12. x = 1 13. 224 14.  15. 0 16. 3465 17.[– 1,7]
15. 0 16. 3465 17.[– 1,7]
22.(本题15分)已知函数 满足
满足 ,且方程f(x) = x有且仅有一个实数根.
,且方程f(x) = x有且仅有一个实数根.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设数列 满足
满足 .求数列
.求数列 的通项公式;
的通项公式;
(Ⅲ)定义 对于(Ⅱ)中的数列
对于(Ⅱ)中的数列 ,令
,令  设
设 为数列
为数列 的前
的前 项和,求证:
项和,求证: .
.
2010年杭州市第一次高考科目教学质量检测
数学理科评分标准
21.(本题15分)某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(Ⅰ)当A、D区域同时用红色鲜花时,求布置花圃的不同方法的种数;
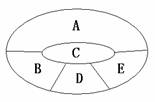 (第21题) |
(Ⅱ)求恰有两个区域用红色鲜花的概率;
(Ⅲ)记 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量 的分布列及其数学期望E
的分布列及其数学期望E .
.
20.(本题14分)已知函数 .
.
(I)若函数 在点
在点 处的切线斜率为4,求实数
处的切线斜率为4,求实数 的值;
的值;
(II)若函数 在区间
在区间 上存在零点,求实数
上存在零点,求实数 的取值如图,
的取值如图,
19.(本题14分) 已知点 和Q( a,0 ),
和Q( a,0 ), 为坐标原点.当
为坐标原点.当 时,
时,
(Ⅰ)若存在点P,使得PO⊥PQ,求实数a的取值范围;
(Ⅱ) 如果a = –1,设向量 与
与 的夹角为
的夹角为 ,求证:cosq ³
,求证:cosq ³  .
.
18.(本题14分)已知函数 (
( ).
).
(Ⅰ)求 的最小正周期,并求
的最小正周期,并求 的最小值.
的最小值.
(Ⅱ)令 ,若
,若 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
17. 已知函数 在区间
在区间 上恰有一个极值点,则实数
上恰有一个极值点,则实数 的取值范围是 .
的取值范围是 .
16. 《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过2000元的不必纳税,超过2000元的部分为全月应纳税所得额.此项税款按下表分段累进计算:
某人一月份应交纳此项税款135元,则他的当月工资、薪金的税后所得是 元.
15.正整数按下列方法分组:{1},{2,3,4},{5,6,7,8,9},{10,11,12,13,14,15,16},…,记第n组各数之和为An ;由自然数的立方构成下列数组:{03,13},{13,23} ,{23,33},{33,43},…,记第n组中两数之和为Bn ,则An – Bn = .
|
全月应纳税所得额 |
税率 |
|
不超过500元的部分 |
5% |
|
超过500元至2000元的部分 |
10% |
|
超过2000元至5000元的部分 |
15% |
|
…… |
… |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com