20.(本小题满分12分)设数列的前项和为，如果为常数，则称数列为“科比数列”．

(Ⅰ)已知等差数列的首项为1，公差不为零，若为“科比数列”，求的通项公式；

(Ⅱ)设数列的各项都是正数，前项和为，若对任意 都成立，试推断数列是否为“科比数列”？并说明理由．

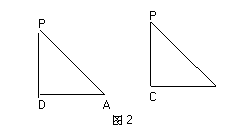
19．(本小题满分12分)如图：在四棱锥P-ABCD中，底面为正方形，PC与底面ABCD垂直(图2为该四棱锥的主视图和侧视图，它们是腰长为6cm的全等的等腰直角三角形.

(Ⅰ)根据图2所给的主视图、侧视图画出相应的俯视图，并求出该俯视图所在的平面图形的面积.

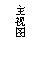
(Ⅱ)图3中，L、E均为棱PB上的点，且，，M、N分别为棱PA 、PD的中点，问在底面正方形的对角线AC上是否存在一点F，使EF//平面LMN. 若存在，请具体求出CF的长度；若不存在，请说明理由.

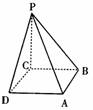
图1

图3

18.(本小题满分12分)某创业投资公司拟投资开发某种新能源产品，估计能获得10万元-1000万元的投资收益.现准备制定一个对科研课题组的奖励方案：奖金y(单位：万元)随投资收益x(单位：万元)的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%.

(Ⅰ)若建立函数模型制定奖励方案，试用数学语言表述公司对奖励函数模型的基本要求；

(Ⅱ)现有两个奖励函数模型：(1)y＝；(2)y＝4lgx－3.试分析这两个函数模型是否符合公司要求？

17．(本小题满分10分)己知向量a，b，函数(a·b).

(Ⅰ)求函数f(x)的定义域和值域；(Ⅱ)求函数f(x)的单调区间.

16.设直角三角形的两直角边的长分别为，斜边长为，斜边上的高为，则有 成立，某同学通过类比得到如下四个结论：

①；②；③ ；④.

其中正确结论的序号是　　　 ；进一步得到的一般结论是　　　　　　　　　　 .

15.2009年北京国庆阅兵式上举行升旗仪式，如图，在坡度为15°的观礼台上，某一列座位与旗杆在同一个垂直于地面的平面上，在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°，且第一排和最后一排的距离为米，则旗杆的高度为　 米 .

14.已知函数的图象恒过定点A，若点A在直线上，则的最小值为　　 ．

13. 已知等差数列的前项和为，且则为 　　

12．若满足满足，则+＝(　　 )

A　　　 　　　　　 B3 　　　　 C 　　　　　　 D4

第Ⅱ卷(非选择题，共90分)

10． 设为坐标原点，点坐标为，若点满足不等式组： 　时，则的最大值的变化范围是(　 )

　 A．[7，8]　　　　　 B．[7，9]　　　　 C．[6，8]　　　　 D．[7，15]

(理)11.已知函数在R上满足，则曲线在点处的切线方程是(　　 )

(A) 　　　(B)　　 (C)　　 (D)