
22.(本小题满分12分)
已知数列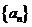 是等差数列,
是等差数列, 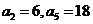 ;数列
;数列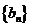 的前n项和是
的前n项和是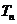 ,且
,且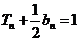 .
.
(Ⅰ) 求数列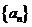 的通项公式;
的通项公式;
(Ⅱ) 求证:数列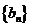 是等比数列;
是等比数列;
(Ⅲ) 记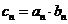 ,求
,求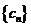 的前n项和
的前n项和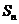 .
.
贵州省乌沙中学09-10学年高三上学期期中考试
21.(本小题满分12分)
已知各项均为正数的数列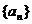 ,
,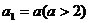 ,
,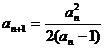 其中
其中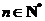 .
.
(Ⅰ)证明 :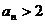 ;
;
(Ⅱ)设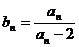 ,①证明 :
,①证明 :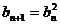 ;
;
②若数列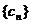 满足
满足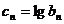 ,求数列
,求数列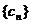 的前
的前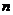 项和
项和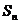 .
.
20.(本小题满分12分)
设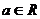 ,函数
,函数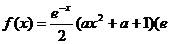 为自然对数的底数).
为自然对数的底数).
(Ⅰ)判断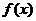 的单调性;
的单调性;
(Ⅱ)若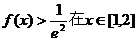 上恒成立,求a的取值范围.
上恒成立,求a的取值范围.
19.(本小题满分12分)
已知袋中装有若干个均匀的红球和白球,从中摸出一个红球的概率是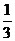 .现从中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
.现从中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
(Ⅰ)求恰好摸5次停止的概率;
(Ⅱ)记5次之内摸到红球的次数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
18.(本小题满分12分)
 已知定义在区间
已知定义在区间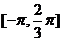 上的函数
上的函数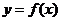 的图象关于直线
的图象关于直线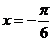 对称,当
对称,当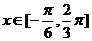 时,函数
时,函数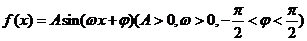 的图象如图.
的图象如图.
(I)求函数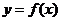 在
在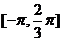 上的表达式;
上的表达式;
(II)求方程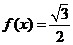 的解.
的解.
17.(本小题满分10分)
函数 的最小正周期为
的最小正周期为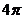 .
.
(Ⅰ)求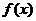 的单调递增区间;
的单调递增区间;
(Ⅱ)在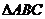 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是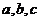 ,且满足
,且满足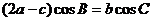 ,求角B的值,并求函数
,求角B的值,并求函数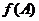 的取值范围.
的取值范围.
16.给出定义:若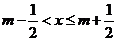 (其中
(其中 为整数),则
为整数),则 叫做离实数
叫做离实数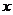 最近的整数,记作
最近的整数,记作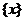 ,即
,即  .在此基础上给出下列关于函数
.在此基础上给出下列关于函数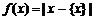 的四个命题:
的四个命题:
①函数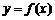 的定义域是R,值域是[0,
的定义域是R,值域是[0,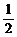 ];
];
②函数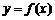 的图像关于直线
的图像关于直线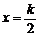 (k∈Z)对称;
(k∈Z)对称;
③函数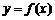 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④ 函数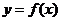 在
在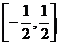 上是增函数;
上是增函数;
则其中真命题是__ .
15.已知命题P:关于x的不等式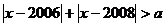 恒成立;命题Q:关于x的函数
恒成立;命题Q:关于x的函数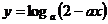 在[0,1]上是减函数.若P或Q为真命题,P且Q为假命题,则实数
在[0,1]上是减函数.若P或Q为真命题,P且Q为假命题,则实数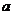 取值范围是 .
取值范围是 .
14.给出命题:①函数 的最小值等于
的最小值等于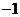 ;
;
②函数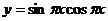 是周期为2的奇函数;
是周期为2的奇函数;
③函数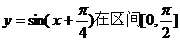 上是单调递增的;
上是单调递增的;
④函数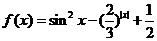 在
在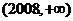 上恒有
上恒有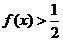 .
.
则正确命题的序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com