
1.(浙江 1)设
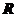 ,
,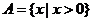 ,
,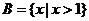 ,则
,则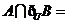 ( B
)
( B
)
A.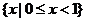 B.
B.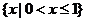 C.
C. D.
D.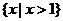
(三)主要数学思想
本章中主要体现的数学思想有等价转化思想、分类讨论思想、函数与方程思想、划归思想、数形结合思想、换元思想。
总之,在复习每一知识点的过程中,都要进一步夯实基础并通过不断训练加以巩固,对考试内容与要求中的各个知识点要让学生心知肚明,特别是与这些知识点有关的常用习题及其解题方法、解题思想要及时归纳总结,掌握基本习题的常用方法,提高学生分析问题、解决问题的能力,提高学生的逻辑思维能力。
(二) 主要数学方法
1.在解不等式中,换元法和图解法是常用的技巧之一。通过换元,可将较复杂的不等式化归为较简单的或基本不等式,通过构造函数、数形结合,则可将不等式的解化归为直观、形象的图形关系,对含有参数的不等式,运用图解法可以使得分类标准明晰。
2.整式不等式(主要是一次、二次不等式)的解法是解不等式的基础,利用不等式的性质及函数的单调性,将分式不等式、绝对值不等式等化归为整式不等式(组)是解不等式的基本思想,分类、换元、数形结合是解不等式的常用方法.方程的根、函数的性质和图象都与不等式的解密切相关,要善于把它们有机地联系起来,相互转化和相互变用。
3.证明不等式的方法灵活多样,但比较法、综合法、分析法仍是证明不等式的最基本方法.要依据题设、题断的结构特点、内在联系,选择适当的证明方法,要熟悉各种证法中的推理思维,并掌握相应的步骤,技巧和语言特点。比较法的一般步骤是:作差(商)→变形→判断符号(值)。
4.证明不等式的方法多样,内容丰富、技巧性较强。在证明不等式前,要依据题设和待证不等式的结构特点、内在联系,选择适当的证明方法。
(一)主要内容
1、 不等式的概念和性质 这是本章内容的基础,是证明不等式和解不等式的主要依据,复习时应高度重视,对每一条性质,要弄清楚条件和结论,注意条件加强和放宽后,条件和结论之间发生的变化;记住了不等式运算法则的结论形式,还要掌握运算法则的条件,避免由于忽略某些限制条件而造成解题失误,掌握证明不等式性质的方法,可以进一步提高逻辑推理能力。
不等式的概念和性质 这是本章内容的基础,是证明不等式和解不等式的主要依据,复习时应高度重视,对每一条性质,要弄清楚条件和结论,注意条件加强和放宽后,条件和结论之间发生的变化;记住了不等式运算法则的结论形式,还要掌握运算法则的条件,避免由于忽略某些限制条件而造成解题失误,掌握证明不等式性质的方法,可以进一步提高逻辑推理能力。
2、一元二次不等式及解法 要理解“三个二次”之间的关系,熟练掌握一元一次不等式的解法、一元二次不等式的解法,这是解其它不等式的基础。会解含参数的一元二次不等式。能将分式不等式转化为整式不等式(组)。
3、简单的线性规划 能从实际问题中抽象出二元一次不等式组。 理解二元一次不等式组表示平面的区域,能够准确的画出可行域。能够将实际问题抽象概括为线性规划问题,培养应用线性规划的知识解决实际问题的能力。
4、均值定理 理解均值不等式的概念,掌握均值不等式的证明过程。能够利用均值不等式求函数的最值问题。能利用均值不等式解答实际问题。
5、不等式的综合应用 能够运用不等式的性质、定理,不等式的解法及不等式的证明有关的数学问题和实际问题。
不等式的性质仍以其他内容为载体进行考查,与不等式的解法都以低中档题出现,估计难度不会加大,主要考查学生基础性的知识和基本解题能力。 线性规划问题,一般是考查最优解问题,或是求参数的取值范围,也有可能在解出现答题中,但仍是低中档题。均值定理的考查往往是和数列、函数等知识相互结合,经常在解答题中某一步出现,可能用到均值定理的变形。
不难发现,在近几年的高考中,不等式这一部分一般不单独命题,而是以其他知识(如函数、集合、充要条件等)为载体进行考查,主要体现它的基础性和工具性。若直接考查,则常以选择题和填空题形式出现。一元二次不等式也是高考重点考察的知识点之一,它的应用范围几乎涉及到高中数学的所有章节,且常考常新,在选择题、填空题、解答题中都有可能出现。线性规划问题的考查主要以选择题和填空题为主,利用基本不等式求函数的最值、证明不等式、比较大小、求代数式的取值范围等问题是该部分重点,也是高考考查的重点,题型多种多样,涉及面广,在解答题中的应用往往有一定的难度。
了解日常生活中的不等关系,了解不等式的有关概念及其分类,掌握不等式的性质及其应用;明确各个性质中结论成立的前提条件。会从实际情境中抽象出一元二次不等式模型;通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系;会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图。了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;了解线性规划的意义并会简单应用。掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单应用。掌握用比较法、分析法、综合法证明简单的不等式。理科在“不等式证明方法”部分,增加了放缩法。
39. (32分)材料一:受美国金融危机的影响,浙江规模以上工业增加值月度增幅从2008年3月的14.9%回落到7、8、9月的9.8%、6.1%、6.4%,增速为10年来最低。 在加剧恶化的经济形势下,浙江的企业家现阶段的情绪有:一是“冬眠论”,对困难“看不到底”,就想着“冬眠”几年,等时机好了再创业;二是“过冬论”,把“宝”押在来年,“寄托于天助,等明年天上掉个馅饼”--“其实,谁会知道冬天有多长”;三是“淘汰论”,认为传统制造业是夕阳产业,“迟早要死,晚死还不如早死,索性袖手旁观。”这些情绪综合的结果是企业家信心指数下滑。
材料二:浙江经济为什么如此受伤?有识之士归结为如下三个原因: 第一,浙江经济以“块状经济、产业集群”为特征,龙头企业与区块内的配套中小企业存在产业链合作关系。你中有我,我中有你的连环担保圈盘根错节,把无数企业的资金链环环相扣地拴在一起。 第二,大型民企,政府在土地、税收、金融、司法保护等方面一意偏袒,导致企业竞争环境恶化,大型民企对政府的依赖性增加,患上了“类国企病”。相反,中小企业面临的最大问题是融资难。第三:粗放发展--浙江经济好比“豆芽菜”:迎着光的方向迅速生长,短时间就长得很高,但根基不扎实,又细又长,大风一起东摇西摆--而浙江制造业迎着国内外低层次需求快速增长,整个规模虽然很大,但附加价值、工艺技术水平较低,抵御风险的能力弱。这也正是浙江在本轮经济危机中反应最为激烈的主因。
材料三:浙江省委、省政府面对金融危机,积极应对。首先是按照党中央、国务院方针政策,从浙江实际出发,扩大内需、增加投资、促进消费、改善民生等等。第二,浙江在应对金融危机过程当中始终把保增长与促调整结合起来,特别是致力于浙江产业结构优化,要素结构优化,需求结构优化和空间布局结构优化,现在看来这一系列保增长、促调整的措施也日益见效。第三,政府、银行、企业一条船、一盘棋,银行、各金融单位全力支持地方经济、各类企业度过难关,特别是让中小企业得到实惠。
(1)根据材料一,请用哲学常识的观点来分析“冬眠论”、 “过冬论”、 “淘汰论”。(12分)
(2)根据材料一、二,请运用经济常识的观点为浙江企业走出困境寻找一些出路和对策。(10分)
(3)材料三体现了政治常识的哪些观点?(8分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com