
9.(2008年湖北卷20).(本小题满分12分)水库的蓄水量随时间而变化.现用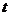 表示时间,以月为单位,年初为起点.根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点.根据历年数据,某水库的蓄水量(单位:亿立方米)关于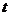 的近似函数关系式为
的近似函数关系式为
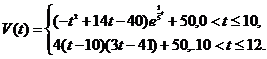
(Ⅰ)该水库的蓄求量小于50的时期称为枯水期.以 表示第i月份(
表示第i月份(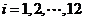 ),问一年内哪几个月份是枯水期?
),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取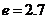 计算).
计算).
解 (1)①当0<t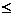 10时,V(t)=(-t2+14t-40)
10时,V(t)=(-t2+14t-40)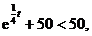
化简得t2-14t+40>0,
解得t<4,或t>10,又0<t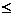 10,故0<t<4.
10,故0<t<4.
②当10<t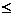 12时,V(t)=4(t-10)(3t-41)+50<50,
12时,V(t)=4(t-10)(3t-41)+50<50,
化简得(t-10)(3t-41)<0,
解得10<t<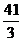 ,又10<t
,又10<t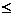 12,故 10<t
12,故 10<t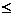 12.
12.
综上得0<t<4,或10<t≤12,
故知枯水期为1月,2月,,3月,4月,11月,12月共6个月.
(2)由(1)知:V(t)的最大值只能在(4,10)内达到.
由V′(t)=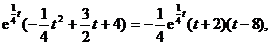 令V′(t)=0,解得t=8(t=-2舍去).
令V′(t)=0,解得t=8(t=-2舍去).
当t变化时,V′(t) 与V (t)的变化情况如下表:
|
t |
(4,8) |
8 |
(8,10) |
|
V′(t) |
+ |
0 |
- |
|
V(t) |
 |
极大值 |
 |
由上表,知V(t)在t=8时取得最大值V(8)=8e2+50=108.32(亿立方米).
故知一年内该水库的最大蓄水量是108.32亿立方米
8.(2008年江苏卷17)某地有三家工厂,分别位于矩形ABCD
的顶点A,B 及CD的中点P处,已知AB=20km,CB=10km ,
为了处理三家工厂的污水,现要在矩形ABCD 的区域上
(含边界),且A,B与等距离的一点O 处建造一个
污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长
为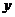 km.
km.
(Ⅰ)按下列要求写出函数关系式:
①设∠BAO=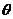 (rad),将
(rad),将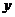 表示成
表示成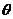 的函数关系式;
的函数关系式;
②设OP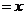 (km) ,将
(km) ,将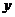 表示成
表示成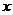 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(Ⅰ)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短.
解 本小题主要考查函数最值的应用.
(Ⅰ)①设AB中点为Q,由条件知PQ 垂直平分AB,若∠BAO=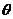 (rad) ,则
(rad) ,则
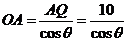 , 故
, 故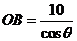 ,又OP=
,又OP=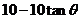 ,
,
所以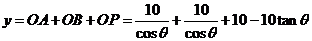 ,
,
所求函数关系式为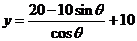
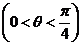
②若OP=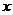 (km) ,则OQ=10-
(km) ,则OQ=10-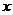 ,所以OA=OB=
,所以OA=OB=
所求函数关系式为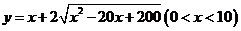
(Ⅱ)选择函数模型①,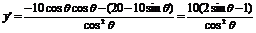
令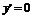 得sin
得sin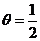 ,因为
,因为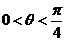 ,所以
,所以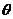 =
=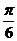 .当
.当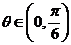 时,
时,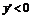 ,
,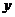 是
是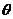 的减函数;当
的减函数;当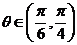 时,
时,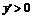 ,y是
,y是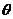 的增函数.所以当
的增函数.所以当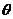 =
=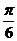 时,
时,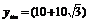 (km)。这时点0位于线段AB 的中垂线上,且距离AB边
(km)。这时点0位于线段AB 的中垂线上,且距离AB边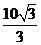 km处。
km处。
7.(2006年北京卷14)某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第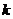 棵树种植在点
棵树种植在点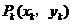 处,其中
处,其中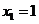 ,
,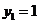 ,当
,当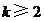 时,
时,

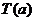 表示非负实数
表示非负实数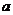 的整数部分,例如
的整数部分,例如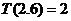 ,
,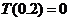 .按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 .
.按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 .
答案 (1,2)(3,402)
6.(2007年上海4)方程 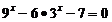 的解是
.
的解是
.
答案 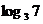
5.(2006年上海春季2)方程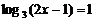 的解
的解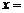 .
.
答案 2
4.某地一年内的气温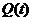 (单位:℃)与时刻
(单位:℃)与时刻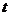 (月份)之间的关系如图所示,已知该年的平均气温为10℃ .令C(t)表示的时间段[0,t]的平均气温,
(月份)之间的关系如图所示,已知该年的平均气温为10℃ .令C(t)表示的时间段[0,t]的平均气温,
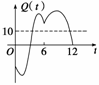 C(t)与t之间的函数关系用下列图象表示,则正确的应该是 ( )
C(t)与t之间的函数关系用下列图象表示,则正确的应该是 ( )
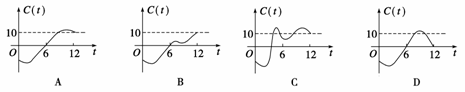
答案 A
解析 由图可以发现当t=6时,C(t)=0,排除C;t=12时,C(t)=10,排除D;t在大于6 的某一段气温超于10,所以排除B,故选A。
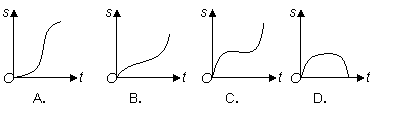
3.(07广东)客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s与时间t之间关系的图象中,正确的是 ( )
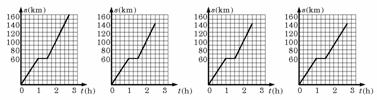
A B C D
答案 C
2.(2008年福建卷12)已知函数y=f(x),y=g(x)的导函数的图象如下图,那么y=f(x),y=g(x)
的图象可能是 ( )
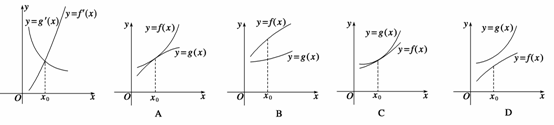
答案 D
1.(2008年全国一2)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一
过程中汽车的行驶路程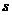 看作时间
看作时间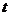 的函数,其图像可能是 ( )
的函数,其图像可能是 ( )
答案 A
7.(2009上海卷文)(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分 .有时可用函数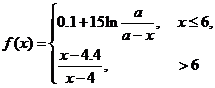
描述学习某学科知识的掌握程度.其中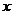 表示某学科知识的学习次数(
表示某学科知识的学习次数(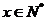 ),
),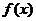 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x 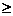 7时,掌握程度的增长量f(x+1)- f(x)总是下降;
7时,掌握程度的增长量f(x+1)- f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],
(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
证明 (1)当 时,
时,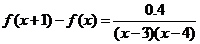
而当 时,函数
时,函数 单调递增,且
单调递增,且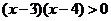
故函数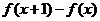 单调递减
单调递减
当 时,掌握程度的增长量
时,掌握程度的增长量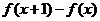 总是下降
总是下降 

(2)有题意可知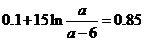
整理得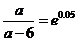
解得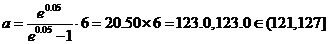 …….13分
…….13分
由此可知,该学科是乙学科……………..14分
2005-2008年高考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com