(五)课堂小结，回顾反思

学生归纳，互相补充，老师总结：

1、理解二分法的定义和思想，用二分法可以求函数的零点近似值，但要保证该函数在零点所在的区间内是连续不断；

2、用二分法求方程的近似解的步骤.

[设计意图]帮助学生梳理知识,形成完整的知识结构.同时让学生知道理解二分法定义是关键，掌握二分法解题的步骤是前提，实际应用是深化.

(四)尝试练习，检验成果

1、下列函数中能用二分法求零点的是(　 ).

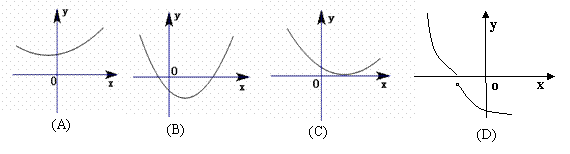
[设计意图]让学生明确二分法的适用范围.

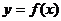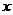2、用二分法求图象是连续不断的函数在∈(1,2)内零点近似值的过程中得到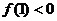,,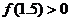,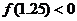则函数的零点落在区间(　 ).

(A)(1,1.25)　　(B)(1.25,1.5)　 (C)(1.5,2)　 (D) 不能确定

[设计意图]让学生进一步明确缩小零点所在范围的方法.

3．借助计算器或计算机，用二分法求方程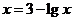在区间(2，3)内的近似解(精确度0.1).

　[设计意图] 进一步加深和巩固对用二分法求方程近似解的理解.

(三)例题剖析，巩固新知

例：借助计算器或计算机用二分法求方程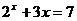的近似解(精确度0.1).

两人一组，一人用计算器求值，一人记录结果；学生讲解缩小区间的方法和过程，教师点评.

本例鼓励学生自行尝试，让学生体验解题遇阻时的困惑以及解决问题的快乐.此例让学生体会用二分法来求方程近似解的完整过程，进一步巩固二分法的思想方法.

思考：

问题(1)：用二分法只能求函数零点的“近似值”吗？

问题(2)：是否所有的零点都可以用二分法来求其近似值？

教师有针对性的提出问题，引导学生回答，学生讨论，交流. 反思二分法的特点，进一步明确二分法的适用范围以及优缺点，指出它只是求函数零点近似值的“一种”方法.

　 　[设计意图]及时巩固二分法的解题步骤,让学生体会二分法是求方程近似解的有效方法.解题过程中也起到了温故转化思想的作用．

(二)师生探究,构建新知

　问题2：假设电话线故障点大概在函数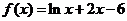的零点位置，请同学们先猜想它的零点大概是什么？我们如何找出这个零点？

　　 1．利用函数性质或借助计算机、计算器画出函数图象，通过具体的函数图象帮助学生理解闭区间上的连续函数，如果两个端点的函数值是异号的，那么函数图象就一定与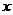轴相交，即方程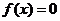在区间内至少有一个解(即上节课的函数零点存在性定理，为下面的学习提供理论基础)．引导学生从“数”和“形”两个角度去体会函数零点的意义，掌握常见函数零点的求法，明确二分法的适用范围．

2．我们已经知道，函数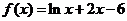在区间(2，3)内有零点，且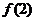＜0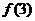，＞0.进一步的问题是，如何找出这个零点？

合作探究：学生先按四人小组探究.(倡导学生积极交流、勇于探索的学习方式，有助于发挥学生学习的主动性)

生：如果能够将零点所在的范围尽量缩小，那么在一定精确度的要求下，我们可以得到零点的近似值.

师：如何有效缩小根所在的区间？

生1：通过“取中点”的方法逐步缩小零点所在的范围．

生2：是否也可以通过“取三等分点或四等分点”的方法逐步缩小零点所在的范围？

师：很好，一个直观的想法是:如果能够将零点所在的范围尽量缩小，那么在一定精确度的要求下，可以得到零点的近似值.其实“取中点”和“取三等分点或四等分点”都能实现缩小零点所在的范围.但是在同样可以实现缩小零点所在范围的前提下，“取中点”的方法比取“三等分点或四等分点”的方法更简便.因此，为了方便，下面通过“取中点”的方法逐步缩小零点所在的范围.

引导学生分析理解求区间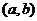的中点的方法．

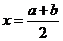合作探究：(学生2人一组互相配合，一人按计算器，一人记录过程．四人小组中的两组比较缩小零点所在范围的结果．)

步骤一：取区间(2，3)的中点2.5，用计算器算得.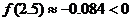

由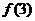＞0，得知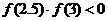，所以零点在区间(2.5，3)内。

　　 步骤二：取区间(2.5，3)的中点2.75，用计算器算得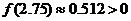.因为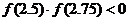，所以零点在区间(2.5，2.75)内.　

结论:由于(2，3)　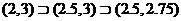，所以零点所在的范围确实越来越小了. 如果重复上述步骤，在一定精确度下，我们可以在有限次重复上述步骤后，将所得的零点所在区间内的任一点作为函数零点的近似值．特别地，可以将区间端点作为函数零点的近似值．

引导学生利用计算器边操作边认识，通过小组合作探究，得出教科书上的表3-2，让学生有更多的时间来思考与体会二分法实质，培养学生合作学习的良好品质．

[学情预设]学生通过上节课的学习知道这个函数的零点就是函数图象与x轴的交点的横坐标，故它的零点在区间(2，3)内．进一步利用函数图象通过“取中点”逐步缩小零点的范围，利用计算器通过将自变量改变步长减少很快得出表3-2，找出零点的大概位置．

[设计意图]从问题1到问题2，体现了数学转化的思想方法，问题2有着承上启下的作用，使学生更深刻地理解二分法的思想，同时也突出了二分法的特点．通过问题2让学生掌握常见函数零点的求法，明确二分法的适用范围．

3.问题3：对于其他函数，如果存在零点是不是也可以用这种方法去求它的近似解呢？

引导学生把上述方法推广到一般的函数，经历归纳方法的一般性过程之后得出二分法及用二分法求函数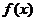的零点近似值的步骤．

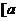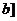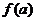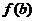
对于在区间，上连续不断且满足·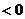的函数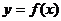，通过不断地把函数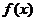的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法．

注意引导学生分化二分法的定义(一是二分法的适用范围，即函数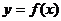在区间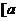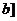，上连续不断，二是用二分法求函数的零点近似值的步骤)．

给定精确度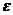，用二分法求函数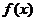的零点近似值的步骤如下：

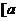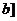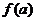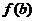
1、确定区间，，验证·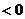，给定精确度；

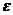2、求区间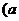，的中点；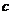

3、计算：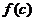

(1)若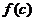=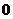，则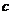就是函数的零点；

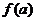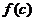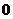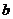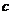(2)若·<，则令=(此时零点)；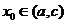

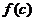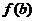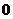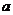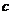(3)若·<，则令=(此时零点)；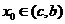

4、判断是否达到精确度：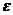

即若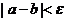，则得到零点零点值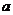(或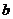)；否则重复步骤2-4．

利用二分法求方程近似解的过程，可以简约地用下图表示．

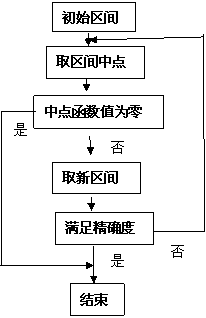
[学情预设] 学生思考问题3举出二次函数外，对照步骤观察函数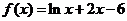的图象去体会二分法的思想．结合二次函数图象和标有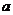、、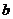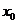的数轴理解二分法的算法思想与计算原理．

[设计意图]以问题研讨的形式替代教师的讲解，分化难点、解决重点，给学生“数学创造”的体验，有利与学生对知识的掌握，并强化对二分法原理的理解．学生在讨论、合作中解决问题，充分体会成功的愉悦．让学生归纳一般步骤有利于提高学生自主学习的能力，让学生尝试由特殊到一般的思维方法．利用二分法求方程近似解的过程，用图表示，既简约又直观，同时能让学生初步体会算法的思想．

(一)创设情境，提出问题

问题1：在一个风雨交加的夜里，从某水库闸房到防洪指挥部的电话线路发生了故障．这是一条10km长的线路，如何迅速查出故障所在？

如果沿着线路一小段一小段查找，困难很多．每查一个点要爬一次电线杆子．10km长，大约有200多根电线杆子呢．

想一想，维修线路的工人师傅怎样工作最合理？

以实际问题为背景，以学生感觉较简单的问题入手，激活学生的思维，形成学生再创造的欲望．注意学生解题过程中出现的问题，及时引导学生思考，从二分查找的角度解决问题．

[学情预设] 学生独立思考，可能出现的以下解决方法：

思路1：直接一个个电线杆去寻找．

思路2：通过先找中点，缩小范围，再找剩下来一半的中点．

老师从思路2入手，引导学生解决问题：

如图，维修工人首先从中点C．查用随身带的话机向两个端点测试时，发现AC段正常，断定故障在BC段，再到BC段中点D，这次发现BD段正常，可见故障在CD段，再到CD中点E来查．每查一次，可以把待查的线路长度缩减一半，如此查下去，不用几次，就能把故障点锁定在一两根电线杆附近．

师：我们可以用一个动态过程来展示一下(展示多媒体课件)．

在一条线段上找某个特定点，可以通过取中点的方法逐步缩小特定点所在的范围(即二分法思想)．

　[设计意图] 从实际问题入手，利用计算机演示用二分法思想查找故障发生点，通过演示让学生初步体会二分法的算法思想与方法, 说明二分法原理源于现实生活，并在现实生活中广泛应用．

2．教学难点：方程近似解所在初始区间的确定，恰当地使用信息技术工具，利用二分法求给定精确度的方程的近似解．

1．教学重点：用“二分法”求方程的近似解，使学生体会函数零点与方程根之间的联系，初步形成用函数观点处理问题的意识．

通过具体实例理解二分法的概念，掌握运用二分法求简单方程近似解的方法，从中体会函数的零点与方程根之间的联系及其在实际问题中的应用；能借助计算器用二分法求方程的近似解，让学生能够初步了解逼近思想；体会数学逼近过程，感受精确与近似的相对统一；通过具体实例的探究，归纳概括所发现的结论或规律，体会从具体到一般的认知过程．

倡导积极主动、勇于探索的学习精神和合作探究式的学习方式；注重提高学生的数学思维能力，发展学生的数学应用意识；与时俱进地认识“双基”，强调数学的内在本质，注意适度形式化；在教与学的和谐统一中体现数学的文化价值；注重信息技术与数学课程的合理整合.