
2.国家利益决定国家关系变化。澳门的回归,是维护国家利益的需要,是我国国家力量增强的结果。
1.国家职能。国家有关部门积极组织澳门回归10周年庆祝活动,是国家履行政治职能、文化职能、社会公共服务职能的体现。
18.本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分12分.
方案一:
 (Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连结AE,可知AC=CB=BE=AE= ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE= ,PB=
,PB= ,
, 

(Ⅲ)解:作AN⊥CM,垂足为N,连结BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角.
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC= ,
,
 . ∴AB=2,
. ∴AB=2,
故所求的二面角为
方法二:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为
A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1, .
.
(Ⅰ)证明:因
又由题设知AD⊥DC,且AP与与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD.
(Ⅱ)解:因


由此得AC与PB所成的角为
(Ⅲ)解:在MC上取一点N(x,y,z),则存在 使
使

要使

 为所求二面角的平面角.
为所求二面角的平面角.



热点题型3 三垂线定理或逆定理作二面角的平面角
如图1,已知ABCD是上.下底边长分别为2和6,高为 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
 (Ⅰ)证明:AC⊥BO1;
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小.
解法一(I)证明 由题设知OA⊥OO1,OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 故可以O为原点,OA、OB、OO1
所在直线分别为 轴、y轴、z轴建立空间直角坐标系,
轴、y轴、z轴建立空间直角坐标系,
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1, )
)
O1(0,0, ).
).
从而
所以AC⊥BO1.
(II)解:因为 所以BO1⊥OC,
所以BO1⊥OC,
由(I)AC⊥BO1,所以BO1⊥平面OAC, 是平面OAC的一个法向量.
是平面OAC的一个法向量.
设 是0平面O1AC的一个法向量,
是0平面O1AC的一个法向量,
由 得
得 .
.
设二面角O-AC-O1的大小为 ,由
,由 、
、 的方向可知
的方向可知
 ,
, >,
>,
所以cos
 ,
, >=
>=
即二面角O-AC-O1的大小是
热点题型4 二面角与探索问题
如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
 (3)AE等于何值时,二面角D1-EC-D的大小为
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
解法(一)
(1)证明:∵AE⊥平面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1= ,AD1=
,AD1= ,
,
故

(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
 ∴∠DHD1为二面角D1-EC-D的平面角.
∴∠DHD1为二面角D1-EC-D的平面角.
设AE=x,则BE=2-x


解法(二):以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)
(2)因为E为AB的中点,则E(1,1,0),
 从而
从而 ,
,
 ,
,
设平面ACD1的法向量为 ,
,
则
也即 ,得
,得 ,从而
,从而 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为

(3)设平面D1EC的法向量 ,∴
,∴
由 令b=1, ∴c=2,a=2-x,
令b=1, ∴c=2,a=2-x,
∴
依题意
∴ (不合,舍去),
(不合,舍去), .
.
∴AE= 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为 .
.
3.转化思想: 例如求一个平面的一条平行线上一点到这个平面的距离较难时,可转化为平行线上其他的点到这个平面的距离
热点题型1 求点到平面的距离
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
(Ⅰ)求BF的长;
(Ⅱ)求点C到平面AEC1F的距离.

解法1:(Ⅰ)过E作EH//BC交CC1于H,则CH=BE=1,EH//AD,且EH=AD.
又∵AF∥EC1,∴∠FAD=∠C1EH.
∴Rt△ADF≌Rt△EHC1. ∴DF=C1H=2.

 (Ⅱ)延长C1E与CB交于G,连AG,
(Ⅱ)延长C1E与CB交于G,连AG,
则平面AEC1F与平面ABCD相交于AG.
过C作CM⊥AG,垂足为M,连C1M,
由三垂线定理可知AG⊥C1M.由于AG⊥面C1MC,且
AG 面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.
面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.

解法2:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2, 4,1),C1(0,4,3).设F(0,0,z).
∵AEC1F为平行四边形,


(II)设 为平面AEC1F的法向量,
为平面AEC1F的法向量,
 .
.


 的夹角为a,则
的夹角为a,则

∴C到平面AEC1F的距离为
热点题型2 定义法作二面角的平面角
 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC= AB=1,M是PB的中点.
AB=1,M是PB的中点.
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小.
2. 点到平面的距离求法有:
①体积法 ②直接法,找出点在平面内的射影
1.二面角的平面角的作法:
①定义 ②三垂线定义 ③ 垂面法
22.(本小题满分12分)
已知点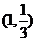 是函数
是函数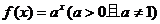 的图象上一点,等比数列
的图象上一点,等比数列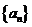 的前
的前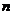 项和为
项和为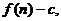 数列
数列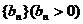 的首项为
的首项为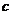 ,且前
,且前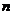 项和
项和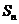 满足
满足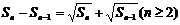
(1)数列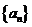 ,
,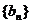 的通项公式;
的通项公式;
(2)若数列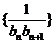 的前
的前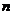 项和为
项和为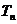 ,问
,问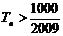 的最小正整数
的最小正整数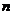 是多少?
是多少?
21. (本小题满分12分)
已知曲线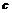 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(-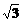 ,0)和F2(
,0)和F2(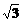 ,0)的距离之和为4.
,0)的距离之和为4.
(1)求曲线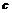 的方程;
的方程;
(2)设过(0,-2)的直线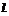 与曲线
与曲线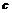 交于C、D两点,且
交于C、D两点,且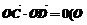 为坐标原点),求直线
为坐标原点),求直线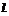 的方程.
的方程.
20.(本小题满分12分)
设函数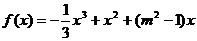 ,其中,
,其中,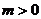
(1)当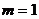 时,曲线
时,曲线 在点
在点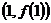 处的切线斜率;
处的切线斜率;
(2)求函数 的单调区间与极值;
的单调区间与极值;
(3)已知函数 有3个不同的零点0,x1,x2,且x1<x2,若对任意的x∈[x1,x2],
有3个不同的零点0,x1,x2,且x1<x2,若对任意的x∈[x1,x2], >
>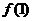 恒成立,求的取值范围.
恒成立,求的取值范围.
19.(本小题满分12分)
已知函数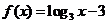 ,设
,设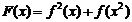
(1)求:当函数f(x)的定义域为[1,3]时,F(x)的最大值及最小值.
(2) 已知条件条件p:函数f(x)的定义域为[1,3],条件 的充分条件,求实数m的取值范围
的充分条件,求实数m的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com