7.设等差数列的前项和为，已知，，则( C )

　 A．－2008　　　　　 B．2008　　　　　　 C．－2010　　　　　 D．2010

[解析]设等差数列的公差为d，则，即.

所以，由已知.

又，则，所以，故选C.

6.如图，正六边形ABCDEF的两个顶点A、D为椭圆的两个焦点，

其余4个顶点在椭圆上，则该椭圆的离心率是　 　　　　　　　　　　　　　　　　　( D )

　 A.　　　　 　　　　　　B.

C.　　　 　　　　　　　D.

[解析]连结AE，则AE⊥DE.设AD＝2c，则DE＝c，AE＝.

椭圆定义，得2a＝AE+ED＝c+c，所以，故选D.

5.在极坐标系中，圆C：关于直线l：对称的充要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　( A )

　 A．k＝1　　　　 　B．k＝－1　　　　　 C．k＝±1　　　　　 D．k＝0

[解析]圆C的直角坐标方程是，直线l的直角坐标方程是y＝x.

若圆C关于直线l对称，则圆心在直线y＝x上，所以，即k＝±1.

又k⁴+4k+1＞0，所以k＝1，故选A.

4.在平面直角坐标系中，i，j分别是与x轴、y轴正方向同向的单位向量，O为坐标原点，设向量＝2i+j，＝3i+kj，若A，O，B三点不共线，且△AOB有一个内角为直角，则实数k的所有可能取值的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　 ( B )

　 A．1　　　　　 　　　B．2　 　　　　　　　C．3　　　　　　 　D．4

[解析]由题设，＝(2，1)，＝(3，k)，则.

当OA⊥OB时，；当OA⊥AB时，；

当OB⊥AB时，(无解).所以k的所有可能取值有2个，故选B.

3.若关于x的方程有两个不等实根，则的取值范围是　　　 ( D )

　 A.　　 B．　　　 　　　C．　　　 　　D．

[解析]据题意，函数的图象与直线有两个不同的交点.由图知，，所以，故选D.

2.设表示不同的直线，表示不同的平面，给出下列4个命题：

　 ①若，且，则；

②若，且∥，则；

③若，则；

④若，且，则.

其中正确命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　 　　　( B )

A．1　　　　　　　 B．2　　　　　　　 C．3　　　　　　　　 D．4

[解析]易知命题①正确；在命题②的条件下，直线可能在平面内，故命题为假；在命题③的条件下，三条直线可以相交于一点，故命题为假；在命题④中，由知，且，由及∥，，得n∥m，同理n∥，故m∥，命题④正确，故选B.

1.已知集合A＝{1，2，a－1}，B＝{0，3，a²+1}，若，则实数a的值为　 ( C )

　 A．±1　　　　　　　 B．1　　　　　 　　C．－1　　　　 　　D．0

[解析]因为，则a²+1＝2，即a＝±1. 但当a＝1时，A＝{1，2，0}，

此时，不合题意，舍去，所以a＝－1，故选C.

21．(本小题满分14分)

　　 已知函数

　 (I)当t=8时，求函数的单调区间 ；

　 (II)求证：当时，对任意正实数x都成立；

　 (III)若存在正实数，使得对任意正实数t都成立，请直接写出满足这样条件的一个的值(不必给出求解过程)

20．(本小题满分14分)

　　 已知椭圆经过点(0，1)，离心率

　 (I)求椭圆C的方程；

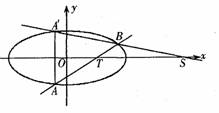　 　 (II)设直线与椭圆C交于A，B两点，点A关于x轴的对称点为A’。试问：当m变化时直线与x轴是否交于一个定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由。

19．(本小题满分13分)

　　　　 在研究性学习小组的一次活动中，甲、乙、丙、丁、戊五位同学被随机地分配承担H，I，J，K四项不同的任务，每项任务至少安排一名同学承担。

　 (I)求甲、乙两人同时承担H任务的概率；

　 (II)求甲、乙两人不同时承担同一项任务的概率；

　 (III)设这五位同学中承担H任务的人数为随机变量，求的分布列及数学期望E。