1、　 物体的受力分析

[例1]以下四种情况中，物体处于平衡状态的有( D )

　　 A、竖直上抛物体达最高点时

　　 B、做匀速圆周运动的物体

　　 C、单摆摆球通过平衡位置时

D、弹簧振子通过平衡位置时

解析：竖直上抛物体在到达最高点时a=g，匀速园周运动物体的加速度a=v²/R，单摆摆球通过平衡位置时，平切向加速度a_切=0，法向加速度a_法=v²/R，合加速度a=v²/R，弹簧振子通过平衡位置时，a=0，故D正确

思考：单摆摆到最高点时是否是平衡状态？

[例2]如图所示，小车M在恒力作用下，沿水平地面做直线运动，由此可以判断(CD)

　 A、若地面光滑，则小车一定受三个力作用

　　 B.若地面粗糙，则小车可能受三个力作用

　　 C若小车做匀速运动，则小车一定受四个力作用

　　 D.若小车加速运动，则小车可能受三个力作用

解析：由于F的垂直分力可能等于重力，因此地面可能对物体无弹力作用，A选项错误。F有竖直分力可能小于重力，地面对物体有弹力作用，若地面粗糙，小车受摩擦力作用，共受四个力，B选项错误。若小车做匀速运动，则水平方向所受的摩擦力与F的水平分力平衡，这时一定受重力、弹力、拉力F和摩擦力四个力的作用，C选项正确；若小车做加速运动，，当地面光滑时，小车受重力和F力的作用或受重力和F力及地面的弹力的作用，D选项正确。

　　 答案：CD

说明：①在常见的几种力中，重力是主动力，而弹力、摩擦力是被动力，其中存在弹力又是摩擦力存在的前提，所以分析受力时应按重力、弹力、摩攘力的顺序去分析．

　　 ②物体的受力情况要与其运动情况相符．因此，常常从物体的运动状态入手，去分析某个力是否存

在．如本例中选项C,D的分析．

3、通常在分析外力对系统作用时，用整体法；在分析系统内各物体之间的相互作用时，用隔离法。有时在解答一个问题时要多次选取研究对象，需要整体法与隔离法交叉使用

规律方法

2、隔离法：把系统分成若干部分并隔离开来，分别以每一部分为研究对象进行受力分根据地，分别列出方程，再联立求解的方法。

1、整体法：以几个物体构成的整个系统为研究对象进行求解的方法。在许多问题中可以用整体法比较方便，但整体法不能求解系统的内力。

3、受力分析的三个判断依据：

①从力的概念判断，寻找施力物体；

②从力的性质判断，寻找产生原因；

③从力的效果判断，寻找是否产生形变或改变运动状态。

2、受力分析的几个步骤．

①灵活选择研究对象：也就是说根据解题的目的，从体系中隔离出所要研究的某一个物体，或从物体中隔离出某一部分作为单独的研究对象，对它进行受力分析．

　　 所选择的研究对象要与周围环境联系密切并且已知量尽量多；对于较复杂问题，由于物体系各部分相互制约，有时要同时隔离几个研究对象才能解决问题．究竟怎样选择研究对象要依题意灵活处理．

②对研究对象周围环境进行分析：除了重力外查看哪些物体与研究对象直接接触，对它有力的作用．凡是直接接触的环境都不能漏掉分析，而不直接接触的环境千万不要考虑进来．然后按照重力、弹力、摩擦力的顺序进行力的分析，根据各种力的产生条件和所满足的物理规律，确定它们的存在或大小、方向、作用点．

③审查研究对象的运动状态：是平衡态还是加速状态等等，根据它所处的状态有时可以确定某些力是否存在或对某些力的方向作出判断．

④根据上述分析，画出研究对象的受力分析图；把各力的方向、作用点(线)准确地表示出来．

1、受力分析的顺序：先找重力，再找接触力(弹力、摩擦力)，最后分析其它力(场力、浮力等)

4、正交分解和等效替代

[例7]如图2－24(a)所示，A、B质量分别为m_A和m_B，叠放在倾角为θ的斜面上以相同的速度匀速下滑，则(　　　 )

　 (A)AB间无摩擦力作用　　　 (B)B受到的滑动摩擦力大小为(m_A+m_B)gsinθ

　 (C)B受到的静摩擦力大小为m_Agsinθ　 (D)取下A物体后，B物体仍能匀速下滑

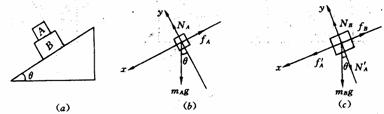解析：隔离A、B，A受力和坐标轴如图(b)所示，由平衡条件得：

　　　 m_Agsinθ－f_A=0…………①　　　 N_A一m_Agcosθ＝0…………②

　　 B受力和坐标轴如图(C)所示，由平衡条件得：

　　　 m_Bgsinθ+f_A^/－f_B=0……………③　　　 N_B一m_Bgcosθ-N_A^/=0…………④

A、　　 B相对静止，f_A为静摩擦力，B在斜面上滑动，f_B为滑动摩擦力

　 f_B＝μN_B…………⑤　 　　　联立①式-⑤式得：

　　　 f_A=m_Agsinθ，f_B=(m_A十m_B)gsinθ，μ=tgθ

　　 取下A后，B受到的滑动磨擦力为f_B＝μm_Bgcosθ=m_Bgsinθ，

　　 B所受摩擦力仍等于重力沿斜面的下滑分力，所以B仍能作匀速直线运动·

　　 综上所述，本题应选择(B)、(C)、(D)。

[例8]某压榨机的结构示意图如图,其中B为固定铰链,若在A处作用于壁的力F,则由于力F的作用，使滑块C压紧物块D，设C与D光滑接触，杆的重力不计，求物体D受到的压力大小是F的几倍？(滑块重力不计)

解析：力F的作用效果是对AC、AB杆产生沿两杆的方向的力F₁、F₂，力F₁产生对C的向左的力和向下的压力。由图可知tanα=100/10=10，F₁=F₂=F/2cosα，N=F₁sinα=Fsinα/2cosα=5F。

试题展示

　　　　　　 物体的受力分析(隔离法与整体法)

基础知识一、物体受力分析方法

把指定的研究对象在特定的物理情景中所受到的所有外力找出来，并画出受力图，就是受力分析。对物体进行正确地受力分析，是解决好力学问题的关键。

3、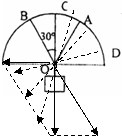用三角形法则分析力的动态变化

[例5]如图所示，将一个重物用两根等长的细绳OA、OB悬挂在半圆形的架子上，在保持重物位置不动的前提下，B点固定不动，悬点A由位置C向位置D移动，直至水平，在这个过程中，两绳的拉力如何变化？

解析：根据力的作用效果，把F分解，其实质是合力的大小方向都不变，一个分力的方向不变，另一个分力的大小方向都在变化，由图中不不看出：OB绳子中的拉力不断增大，而OA绳中的拉力先减小后增大，当OA与OB垂直时，该力最小。

[例6]如图所示，质量为m的球放在倾角为α的光滑斜面上，试分析挡板AO与斜面间的倾角β多大时，AO所受压力最小？

　　 解析：虽然题目问的是挡板AO的受力情况，但若直接以挡板为研究对象，因挡板所受力均为未知力，将无法得出结论．

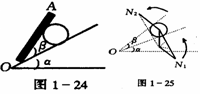　　 以球为研究对象，球所受重力对也产生的效果有两个：对斜面产生了压力N₁，对挡板产生了压力N₂．根据重力产生的效果将重力分解，如图所示．

当挡板与斜面的夹角β由图示位置变化时．N₁大小改变．但方向不变．始终与斜面垂直：N₂的大小、方向均改变(图1一25中画出的一系列虚线表示变化的N₂)．由图可看出．当N₂与N₁垂直即β＝90⁰时，挡板AO所受压力最小，最小压力N_2min=mgsinα．

也可用解析法进行分析，根据正弦定理有N₂/sinα=mg/sinβ，所以N₂=mgsinα/sinβ。而其中mgsinα是定值，N₂随β的变化而变化

当β<90⁰时，β↑→sinβ↑→N₂↓；当β>90⁰时，β↑→sinβ↓→N₂↑；当β=90⁰时，N₂有最小值N_2min=mgsinα；

说明：(1)力的分解不是随意的，要根据力的实际作用效果确定力的分解方向．

(2)利用图解法来定性地分析一些动态变化问题，简单直观有效，是经常使用的方法，要熟练掌握．

物体受到多个力作用时求其合力，可将各个力沿两个相互垂直的方向直行正交分解，然后再分别沿这两个方向求出合力，正交分解法是处理多个力作用用问题的基本方法，步骤为：

①正确选择直角坐标系，一般选共点力的作用点为原点，水平方向或物体运动的加速度方向为X轴，使尽量多的力在坐标轴上。

②正交分解各力，即分别将各力投影在坐标轴上，分别求出坐标轴上各力投影的合力。

Fx=F1x+F2x+…+Fnx　　　　　 Fy=F1y+F2y+…+Fny

③共点力合力的大小为F=，合力方向与X轴夹角

规律方法1、基本规律与方法的应用

[例1]两个力的合力与这两个力的关系，下列说法中正确的是：( CD )

A、　 合力比这两个力都大

B、　 合力至少比两个力中较小的力大

C、　 合力可能比这两个力都小

D、　 合力可能比这两个力都大

解析：(1)公式法：由合力公式F=得

①　　　 当θ=0⁰时，F=F₁+F₂；②当θ=180⁰时，F=|F₁－F₂|；③当θ=90⁰时，F=；④当θ=120⁰且F₁=F₂时，F=F₁=F₂

可见合力可能比任何一个分力都大，也可能比任何一个分力都小，也可能等于每一个分力

(2)图象法：由三角形定则知，合力与分力的关系实际上是三角形的一个边与其它两个边的关系。由两边之和大于第三边，两边之差小于第三边，同时考虑到两个分力同向或反向的情况，合力的取值范围为| F₁－F₂|≤F≤(F₁+F₂)，故答案为CD

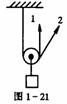[例2]施用一动滑轮将一物体提起来，不计滑轮与绳的质量及其间的摩擦力，则(BCD)

　　 A．总可以省力一半；　　　　　　 B．最大省力一半；

　　 C．拉力可能大于被提物体的重量；　 D．拉力可能等于被提物体的重量；　　　　　　　　　　

　　 解析：如图1－21所示，当拉力沿竖直方向时．省力一半，当沿2的方向上提时拉力肯定大于物体重力一半．所以A错B对，当两绳间夹角等于120⁰时拉力等于物体重量，所以D对，当夹角大于120⁰时，拉力大于物体重量，所以c对．

说明：力是矢量，它的加减不是简单的代数加减；不共线的两个共点力与它们的合力构成三角形，利用正、余弦定理，三角形几何知识来分析相关问题，直观简捷！

[例3] A的质量是m，A、B始终相对静止，共同沿水平面向右运动。当a₁=0时和a₂=0.75g时，B对A的作用力F_B各多大？　　　　　　　　　　　　　　　　　　　　　

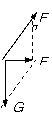解：一定要审清题：B对A的作用力F_B是B对A的支持力和摩擦力的合力。而A所受重力G=mg和F_B的合力是F=ma。

　　 当a₁=0时，G与 F_B二力平衡，所以F_B大小为mg，方向竖直向上。

　　 当a₂=0.75g时，用平行四边形定则作图：先画出重力(包括大小和方向)，再画出A所受合力F的大小和方向，再根据平行四边形定则画出F_B。由已知可得F_B的大小F_B=1.25mg，方向与竖直方向成37^o角斜向右上方。

2、 用图象法求合力与分力

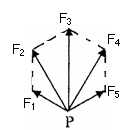[例4]设有五个力同时作用在质点P，它们的大小和方向相当于正六边形的两条边和三条对角线，如图所示，这五个力中的最小力的大小为F，则这五个力的合力等于(　)

　A、3F　 B、4F　 C、5F　 D、6F

解析：由正六边形的特点可知，当最小的力为F时，最大的力为2F，不难推出F₁与F₄合力大小为F₃，即2F，方向也与F₃相同，F₂与F₅的合力大小为F₃，即2F，方向也与F₃相同，故最后合力为6F。用力的三角形法则也可得出同样的结论。