
7.答案:C
[解析]对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
6.解:设切点 ,则
,则 ,又
,又
 .故答案选B
.故答案选B
5.答案:C [解析]取BC的中点E,则 面
面 ,
, ,因此
,因此 与平面
与平面 所成角即为
所成角即为 ,设
,设 ,
, ,即有
,即有 .
.
3.解:  是单位向量
是单位向量
 故选D.
故选D.
.解:  函数
函数 的图像关于点
的图像关于点 中心对称
中心对称


 由此易得
由此易得 .故选A
.故选A
2.答案:C [解析]对于“ 且
且 ”可以推出“
”可以推出“ 且
且 ”,反之也是成立的
”,反之也是成立的
1.答案:B [解析]
对于 ,因此
,因此
 .
.
19.设函数 有两个极值点
有两个极值点 ,且
,且 ,
,
求 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性;
|
 平面
平面 ,
,
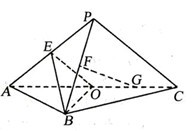 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别为
分别为 ,
,
 ,
, 的中点,
的中点, ,
, .
.
(I)设 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(II)证明:在 内存在一点
内存在一点 ,使
,使 平面
平面 .
.
|
 ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(1)求椭圆C的方程;
(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,
证明直线EF的斜率为定值,并求出这个定值。
|
 ,
, ,
,
其中 .
.
(I)设函数 .若
.若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(II)设函数 是否存在
是否存在 ,对任意给定的非零实数
,对任意给定的非零实数 ,存在惟一的非零实数
,存在惟一的非零实数 (
( ),使得
),使得 成立?若存在,求
成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
数 学试题(理)答案
学试题(理)答案
18.在 数列
数列 中,
中, ,
,
(I)设 ,求数列
,求数列 的通项公式;
的通项公式;
(II)求数列 的前
的前 项和
项和
17.在 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为 、
、 、
、 ,已知
,已知 ,且
,且 求b
求b
16. 14.已知数列 满足:
满足: 则
则 ________;
________; =_________.
=_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com