
19.(本题满分16分)
已知函数f(x)=alnx+x2(a为实常数).
(1)若a=-2,求证:函数f(x)在(1,+.∞)上是增函数;
(2)求函数f(x)在[1,e]上的最小值及相应的x值;
(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
18.(本小题满分16分)
设椭圆 的左焦点为F,上顶点为A,过点A且与AF垂直的光线经椭圆的右准线反射,反射光线与直线AF平行.
的左焦点为F,上顶点为A,过点A且与AF垂直的光线经椭圆的右准线反射,反射光线与直线AF平行.
(1)求椭圆的离心率;
(2)设入射光线与右准线的交点为B,过A,B,F三点的圆恰好与直线3x一y+3=0相切,求椭圆的方程.
17.(本小题满分14分)
在直角坐标系xoy中,若角 的始边为x轴的非负半轴,终边为射线l:y=
的始边为x轴的非负半轴,终边为射线l:y= x (x≥0).
x (x≥0).
(1)求 的值;
的值;
(2)若点P,Q分别是角 始边、终边上的动点,且PQ=4,求△POQ面积最大时,点P,Q
始边、终边上的动点,且PQ=4,求△POQ面积最大时,点P,Q
的坐标.
16.(本小题满分14分)
如图,四边形ABCD为矩形,BC上平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
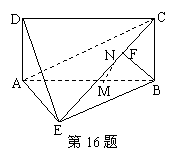 (2)设点M为线段AB的中点,点N为线段CE的中点.
(2)设点M为线段AB的中点,点N为线段CE的中点.
求证:MN∥平面DAE.


15.(本小题满分14分)
已知z,y之间的一组数据如下表:
|
x |
1 |
3 |
6 |
7 |
8 |
|
y |
1 |
2 |
3 |
4 |
5 |
(1)从x ,y中各取一个数,求x+y≥10的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为 与
与 ,试利
,试利
用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
14.设函数 ,方程f(x)=x+a有且只有两相不等实数根,则实a的取值范围为
.
,方程f(x)=x+a有且只有两相不等实数根,则实a的取值范围为
.
13.已知数列{an}共有m项,记{an}的所有项和为s(1),第二项及以后
所有项和为s(2),第三项及以后所有项和为s(3),…,第n项及以后所有项和为s(n),若s(n)是首项为1,公差为2的等差数列的前n项和,则当n<m时,an = .
12.如图,半径为10 cm的圆形纸板内有一个相同圆心的半径为1 cm的
小圆.现将半径为1 cm的一枚硬币抛到此纸板上,使硬币整体随机
落在纸板内,则硬币落下后与小圆无公共点的概率为 .
11.已知函数f(x)=  sinx+cosx,则
sinx+cosx,则 =
.
=
.
10. 如图,已知双曲线以长方形ABCD的顶点A,B为左、右焦点,且过C,D两顶点.若AB=4,BC=3,则此双曲线的标准方程为
.
如图,已知双曲线以长方形ABCD的顶点A,B为左、右焦点,且过C,D两顶点.若AB=4,BC=3,则此双曲线的标准方程为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com