2、线段成比例及有关概念的意义：

1)　　　 成比例线段：在四条线段中，如果其中两条线段的比等于另外两条线段的　

比，那么这四条线段叫做成比例线段，简称比例线段。已知四条线段a、b、c、d，如果或a：b=c：d，那么a、b、c、d叫做成比例的项，线段a、d叫做比例外项，线段b、d叫做比例内项，线段d叫做a、b、c的第四比例项，当比例内项相同时，即或a：b=b：c，那么线段b叫做线段a和c的比例中项．

2)　　　 黄金分割：在线段AB上有一点C，若AC：AB=BC：AC，则C点就是AB的

黄金分割点．一条线段有两个黄金分割点。

1、　 线段比的含义：如果选用同一长度单位得两条线段a、b的长度分别为m、n，

那么就说这两条线段的比是a：b=m：n，或写成，和数的一样，两条线段的比a、b中，a叫做比的前项 b叫做比的后项．

　　　　 　　　　　注意：①针对两条线段；

②两条线段的长度单位相同，但与所采用的单位无关；

③其比值为一个不带单位的正数．

20．(1)2，1；(2)3；(3)当时，没有公共点；当时，有无数个公共点；当时，有唯二个公共点；当时，有唯一公共点；当时，没有公共点．　 21．(1)2；(2)如图①所示；(3)PQ变换与QP变换是不相同的变换，如图②、③所示．

18．(1)连OA、DE，可得Rt△ADO≌Rt△AEO，OD＝OE，所以OA垂直平分DE．(2)30^o．　 19．(1)证△AOF≌△COE；(2)证EF∥AB；(3)EF⊥AB时，四边形BEDF为菱形，旋转角为45^o．

15．略．　 16．(1)略；(2)．　 17．(1)轴对称，中心对称；(2)略．

9．4或6　 10．　 11．45^o　 12．　 13．60　 14．(1，3)

1．D　 2．B　 3．A　 4．A　 5．D　 6．D　 7．A　 8．B

21．如图①，在66的方格纸中，给出如下三种变换：P变换，Q变换，R变换．

将图形F沿轴向右平移1格得图形F₁，称为作1次P变换；将图形F沿轴翻折得图形F₂，称为作1次Q变换；将图形F绕坐标原点顺时针旋转90^o得图形F₃，称为作1次R变换．规定：PQ变换表示先作1次Q变换，再作1次P变换；QP变换表示先作1次P变换，再作1次Q变换；Rⁿ变换表示作次R变换．

解答下列问题：

(1)作R⁴变换相当于至少作______________次Q变换；

(2)请在图②中画出图形F作R²⁰⁰⁷变换后得到的图形F₄；

(3)PQ变换与QP变换是否是相同的变换？请在图③中画出PQ变换后得到的图形F₅，在图④中画出QP变换后得到的图形F₆．

图①　　　　　　　　　　 图②　　　　　　　　　 图③　　　　　　　　 图④

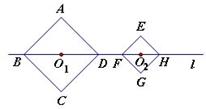
20．如图，正方形ABCD和正方形EFGH的边长分别为和，对角线BD、FH都在直线上，O₁、O₂分别是两个正方形的中心，线段O₁O₂的长叫做两个正方形的中心距．当中心O₂在直线上平移时，正方形EFGH也随之平移，在平移时正方形EFGH的形状、大小没有改变．

　　 (1)计算：O₁D＝___________，O₂F＝____________；

　　 (2)当O₂在直线上平移到两个正方形只有一个公共点时，中心距O₁O₂＝________；

　　 (3)随着中心O₂在直线上的平移，两个正方形的公共点的个数还有哪些变化？并求出相对应的中心距的值或取值范围(不必写出计算过程)．

19．如图①、②、③，□ABCD中，AB⊥AC，AB＝1，BC＝，对角线AC、BD相交于点O，将直线AC绕点O顺时针旋转．分别交BC、AD于点E、F．

(1)试说明在旋转过程中，线段AF与EC总保持相等；

(2)如图②，证明：当旋转角为90^o时，四边形ABEF是平行四边形？

(3)在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由，并求出此时AC绕点O顺时针旋转的度数．

　　　　　　　　　　　 图①　　　　　　　　　　　 图②　　　　　　　　　　　　 图③