15．1.5．　 16．．　 17．17.3米．

9．75 　10．　 11．0.8　 12．　 13．4　 14．或

1．D　 2．B　 3．C　 4．A　 5．A　 6．B　 7．C　 8．A

9、此处只给出两种方法(还有其他方法)。

(1)如下图.

延长CB到D，使BD=AB，连接AD，则∠D=15°。

tan15°===2－。

(2)如下图，延长CA到E，使CE=CB，

连接BE，则∠ABE=15°。　 ∴tan15°=2－。

B组

8、如图，AE⊥CD于点E，AB=CE=0.8，AE=BC=3。

在直角三角形ADE中，cotα=，DE=AE×cotα=3cotα．

　　 因为α≤45°，所以cotα≥1，所以DE>3．

CD=CE+DE>3.8(米)。

因此，避雷针最少应该安装3.8米高。

7、略。

6、提示：作AD⊥BC，垂足为D。

5、解：如下图，作DF⊥BC于点F．由条件可得四边形AEFD是矩形，AD=EF=10．

　　 AB的坡角为1：1，所以=1，所以BE=10．同理可得CF=10．

　　 里口宽BC=BE+EF+FC=30(厘米)．

　　 截面积为×(10+30)×10=200(平方厘米)．

4、如图，∠DAB=∠BCD=90°，∠ADC=60°，AB=2，BC=11，延长AB，DC交于E．

在Rt△AED中，∠A=90°，∠ADE=60°则∠AED=30°

又在△BEC中，∠C=90°，BC=11

∴BE=11×2=22，AE=22+2=24

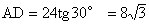
再在Rt△ABD中，∵∠A=90°

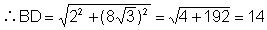
3、如图，在△ACE中，∠E=90°，∠CAE=30°，EC=15米．

则AC=15×2=30(米)

又∵DE=AEtg15°=25.98×0.267=6.94(米)

∴乙楼DC=CE+ED =15+6.94=21.94(米)

答：乙楼的高为21.94米．