
19.(本小题满分13分) 某隧道长为2150m,通过隧道的车速不能超过 m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最大速度为40m/s),匀速通过该隧道,设车队的速度为
m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最大速度为40m/s),匀速通过该隧道,设车队的速度为 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当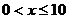 时,相邻两车之间保持20 m的距离;当
时,相邻两车之间保持20 m的距离;当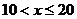 时,相邻两车之间保持
时,相邻两车之间保持 m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为 .
.
(I)将 表示为
表示为 的函数;
的函数;
(II)求车队通过隧道时间 的最小值及此时车队的速度.
的最小值及此时车队的速度.
18.(本小题满分13分) 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.
 (Ⅰ)确定点G的位置;
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小.
17.(本小题满分13分)数列 满足
满足
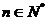 ,先计算前4项后,猜想
,先计算前4项后,猜想 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
16、(本小题满分13分)已知函数 在x=3时取得极值-54
在x=3时取得极值-54
(Ⅰ)求a,b的值
(Ⅱ)求曲线y= 与x轴围成图形的面积
与x轴围成图形的面积
15.设 ,当
,当 时取得极大值,当
时取得极大值,当 时取得极小值,则
时取得极小值,则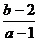 的取值范围为_________
的取值范围为_________
14.已知等差数列 中,有
中,有 成立.类似地,在等比数列
成立.类似地,在等比数列 中,有_________________________________成立.
中,有_________________________________成立.
13.已知 ,则当
,则当 取最大值时,
取最大值时, =_____________.
=_____________.
12.函数 在
在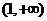 上为增函数,则
上为增函数,则 的取值范围是
.
的取值范围是
.
11.若向量 ,且
,且 与
与 的夹角余弦为_____________.
的夹角余弦为_____________.
10.对于直角坐标平面内的任意两点A(x ,
, y
y )、B(x
)、B(x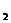 ,y
,y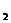 ),定义它们之间的一种“距离”:
),定义它们之间的一种“距离”:
‖AB‖=︱x -x
-x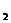 ︱+︱y
︱+︱y -y
-y ︱。给出下列三个命题:
︱。给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖ +‖CB‖
+‖CB‖ =‖AB‖
=‖AB‖ ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷 非选择题(共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com