17、已知函数f(x)=kx²-2x-4在[5，20]上是单调函数，求实数k的取值范围。

16、已知函数f(x)=ax²-2ax+3-b(a≠0)在[1,3]有最大值5和最小值2，求a、b的值。

15、x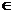R时，讨论一次函数y=mx+b的单调性，并利用定义证明你的结论。

14、如果奇函数f(x)在[2，5]上是减函数，且最小值是-5，那么f(x)在[-5,-2]上的最大值为

13、函数f(x)=1-的单调递增区间是

12、函数y=-x²在(0，+∞)上是减函数，则a的取值范围是

11、函数y=-|x|在[a，+∞)上是减函数，则a的取值范围是

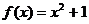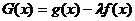20．(14分)已知函数，且，，试问，是否存在实数，使得在上为减函数，并且在上为增函数.

19．(14分)在经济学中，函数的边际函数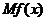为，定义为，某公司每月最多生产100台报警系统装置。生产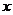台的收入函数为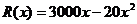(单位元)，其成本函数为(单位元)，利润的等于收入与成本之差.

①求出利润函数及其边际利润函数；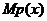

②求出的利润函数及其边际利润函数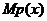是否具有相同的最大值；

③你认为本题中边际利润函数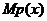最大值的实际意义.

18．(12分))函数在区间上都有意义，且在此区间上

①为增函数，；

②为减函数，.

判断在的单调性，并给出证明.