
21.(12分)椭圆 双曲线
双曲线 两渐近线为
两渐近线为 过椭圆
过椭圆 的右焦点
的右焦点 作直线
作直线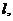 使
使 又设
又设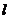 与
与 交于点
交于点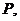
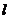 与
与 两交点自上而下依次为
两交点自上而下依次为
(1)当 与
与 夹角为
夹角为 双曲线焦距为4时,求椭圆
双曲线焦距为4时,求椭圆 的方程及其离心率;
的方程及其离心率;
(2)若 求
求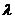 的最小值.
的最小值.
20.(12分)等比数列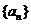 单调递增,且满足:
单调递增,且满足:
(1)求数列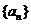 的通项公式;
的通项公式;
(2)数列 满足:
满足: 且
且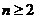 时,
时, 成等比数列,
成等比数列, 为
为 前
前 项和,
项和,
证明:
19.(12分)某渔业公司年初用98万元购进一艘渔船用于捕捞,第一年需各种费用12万元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的总收入为50万元.
(1)该船投入捕捞后第几年开始赢利?
(2)该船投入捕捞多少年后,赢利总额达到最大值?
18.(13分)已知

(1)若 求
求 的取值范围;
的取值范围;
(2)当 在(1)给的范围内取值时,求
在(1)给的范围内取值时,求 的最大值.
的最大值.
17.(13分)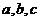 分别为
分别为 内角
内角 的对边,
的对边,


(1)求
(2)若 求
求 的面积.
的面积.
16.(13分)已知抛物线 焦点
焦点 到准线
到准线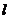 的距离为2.
的距离为2.
(1)求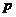 的值;
的值;
(2)过点 作斜率为1的直线
作斜率为1的直线 交抛物线于点
交抛物线于点 求
求
15.椭圆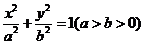 与
与 轴负半轴交于点
轴负半轴交于点
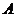 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线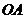 交椭圆于另一点
交椭圆于另一点 椭圆左焦点为
椭圆左焦点为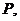 连接
连接 交
交 于点
于点 若
若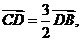 则椭圆的离心率等于________________.
则椭圆的离心率等于________________.
14.已知数列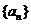 对于任意的
对于任意的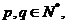 有
有 若
若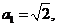 则
则 _______________.
_______________.
13.已知
 与
与 的夹角为45°,若
的夹角为45°,若 则实数
则实数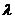 的取值范围是_____.
的取值范围是_____.
12.已知 是椭圆
是椭圆 的两个焦点,过
的两个焦点,过 的直线交椭圆于点
的直线交椭圆于点 若
若 则
则 的值为_____________.
的值为_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com