
20、如图,在直三棱柱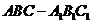 中,
中,
 ,
,
点 是
是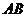 中点。
中点。
⑴求证: 平面
平面 ;
;
 ⑵求异面直线
⑵求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
⑶求二面角 的正切值。
的正切值。
19、已知函数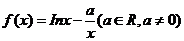 。
。
⑴当 时,讨论
时,讨论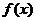 在定义域上的单调性;
在定义域上的单调性;
⑵若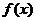 在区间
在区间 上的最小值是
上的最小值是 求实数
求实数 的值。
的值。
18、为了美化校园环境,学校打算在兰蕙广场上建造一个绚丽多彩的矩形花园,
中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为2米,如图所示,设矩形花坛的长为 ,宽为
,宽为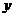 ,整个矩形花园面积为
,整个矩形花园面积为 。
。
⑴试用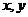 表示S;
表示S;
⑵为了节约用地,当矩形花坛的长为多少米时,新建矩形花园占地最少,
 占地多少平米?
占地多少平米?
17、数列 的前项和为
的前项和为 且
且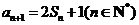 .
.
⑴求数列 的通项公式;
的通项公式;
⑵等差数列 的各项均为正数,其前项和为
的各项均为正数,其前项和为 ,
,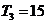 ,
,
又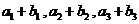 成等比数列,求
成等比数列,求 .
.
共75分,解答应写出文字说明、证明过程或演算步骤。
16、已知向量
又二次函数 的图象开口向上,其对称轴为
的图象开口向上,其对称轴为 。
。
⑴分别求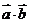 和
和 的取值范围
的取值范围
⑵当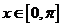 时,求不等式
时,求不等式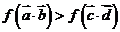 的解集。
的解集。
15、若直线 平分圆
平分圆 则:
则:
⑴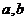 满足的条件是
;
满足的条件是
;
⑵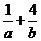 的最小值是
。
的最小值是
。
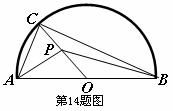
14、如图,半圆的直径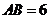 ,
, 为圆心,
为圆心, 为半圆上不同于
为半圆上不同于 的任意一点,若
的任意一点,若 为半径
为半径 上的动点, 则
上的动点, 则 的最小值是__________.
的最小值是__________.
13、设 且
且 ,若
,若 恒成立,
恒成立,
则实数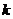 的取值范围是
的取值范围是
12、若一个底面为正三角形,侧棱与底面垂直的棱柱的三视图如下图所示,
则这个棱柱的体积为

11、等差数列 中,
中,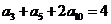 ,则此数列的前
,则此数列的前 项的和等于
项的和等于
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com