
24.(2009年上海卷理)已知三个球的半径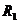 ,
, ,
, 满足
满足 ,则它们的表面积
,则它们的表面积 ,
, ,
,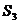 ,满足的等量关系是___________.
,满足的等量关系是___________.
[答案]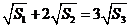
[解析] ,
, ,同理:
,同理:
 ,即R1=
,即R1= ,R2=
,R2=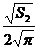 ,R3=
,R3= ,由
,由 得
得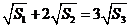
23. (2009年上海卷理)如图,若正四棱柱
(2009年上海卷理)如图,若正四棱柱 的底面连长为2,高 为4,则异面直线
的底面连长为2,高 为4,则异面直线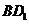 与AD所成角的大小是______________(结果用反三角函数表示).
与AD所成角的大小是______________(结果用反三角函数表示).
[答案]
[解析]因为AD∥A1D1,异面直线BD1与AD所成角就是BD1与A1D1所在角,即∠A1D1B,
由勾股定理,得A1B=2 ,tan∠A1D1B=
,tan∠A1D1B= ,所以,∠A1D1B=
,所以,∠A1D1B= 。
。
22.(2009福建卷文)如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为 。则该集合体的俯视图可以是
。则该集合体的俯视图可以是

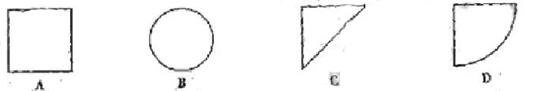
解析 解法1 由题意可知当俯视图是A时,即每个视图是变边长为1的正方形,那么此几何体是立方体,显然体积是1,注意到题目体积是 ,知其是立方体的一半,可知选C.
,知其是立方体的一半,可知选C.
解法2 当俯视图是A时,正方体的体积是1;当俯视图是B时,该几何体是圆柱,底面积是 ,高为1,则体积是
,高为1,则体积是 ;当俯视是C时,该几何是直三棱柱,故体积是
;当俯视是C时,该几何是直三棱柱,故体积是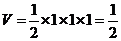 ,当俯视图是D时,该几何是圆柱切割而成,其体积是
,当俯视图是D时,该几何是圆柱切割而成,其体积是 .故选C.
.故选C.
21.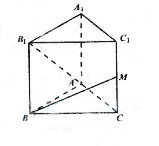 (2009四川卷理)如图,已知正三棱柱
(2009四川卷理)如图,已知正三棱柱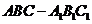 的各条棱长都相等,
的各条棱长都相等,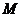 是侧 棱
是侧 棱 的中点,则异面直线
的中点,则异面直线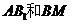 所成的角的大小是
。
所成的角的大小是
。
[考点定位]本小题考查异面直线的夹角,基础题。
解析:不妨设棱长为2,选择基向量 ,则
,则
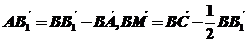
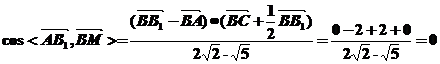 ,故填写
,故填写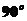 。
。
法2:取BC中点N,连结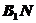 ,则
,则 面
面 ,∴
,∴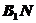 是
是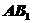 在面
在面 上的射影,由几何知识知
上的射影,由几何知识知 ,由三垂线定理得
,由三垂线定理得 ,故填写
,故填写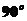 。
。
20.(2009陕西卷文)如图球O的半径为2,圆 是一小圆,
是一小圆, ,A、B是圆
,A、B是圆 上两点,若
上两点,若 =
=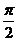 ,则A,B两点间的球面距离为
.
,则A,B两点间的球面距离为
.
答案: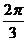

解析:由 ,
, =2由勾股定理在
=2由勾股定理在 中
中
则有 , 又
, 又 =
=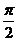 则
则 所以在
所以在 ,
,
 ,则
,则 ,那么
,那么
由弧长公式 得
得 .
.
19. (2009四川卷文)如图,已知正三棱柱
(2009四川卷文)如图,已知正三棱柱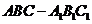 的各条棱长都相等,
的各条棱长都相等,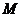 是侧棱
是侧棱 的中点,则异面直线
的中点,则异面直线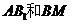 所成的角的大小是
。
所成的角的大小是
。
[答案]90°
[解析]作BC的中点N,连接AN,则AN⊥平面BCC1B1,连接B1N,则B1N是AB1在平面BCC1B1的射影,∵B1N⊥BM,∴AB1⊥BM.即异面直线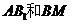 所成的角的大小是90°
所成的角的大小是90°
14.(2009全国卷Ⅰ文)已知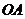 为球
为球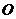 的半径,过
的半径,过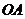 的中点
的中点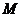 且垂直于
且垂直于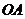 的平面截球面得到圆
的平面截球面得到圆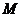 ,若圆
,若圆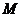 的面积为
的面积为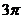 ,则球
,则球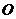 的表面积等于__________________.
的表面积等于__________________.
[解析]本小题考查球的截面圆性质、球的表面积,基础题。
解:设球半径为 ,圆M的半径为
,圆M的半径为 ,则
,则 ,即
,即 由题得
由题得 ,所以
,所以 。
。
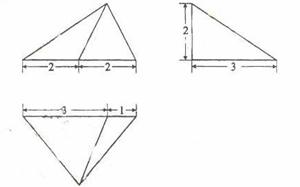
18.(2009辽宁卷理)设某几何体的三视图如下(尺寸的长度单位为m)。
则该几何体的体积为 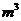
[解析]这是一个三棱锥,高为2,底面三角形一边为4,这边上的高为3, 体积等于 ×2×4×3=4
×2×4×3=4
[答案]4
17.(2009全国卷Ⅱ理)设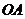 是球
是球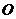 的半径,
的半径,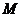 是
是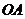 的中点,过
的中点,过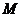 且与
且与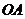 成45°角的平面截球
成45°角的平面截球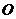 的表面得到圆
的表面得到圆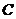 。若圆
。若圆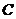 的面积等于
的面积等于 ,则球
,则球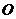 的表面积等于
的表面积等于  .
.
解:设球半径为 ,圆
,圆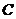 的半径为
的半径为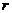 ,
,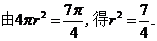
 因为
因为 。由
。由 得
得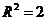 .故球
.故球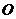 的表面积等于
的表面积等于 .
.
16.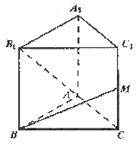 (2009四川卷文)如图,已知正三棱柱
(2009四川卷文)如图,已知正三棱柱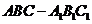 的各条棱长都相等,
的各条棱长都相等,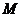 是侧棱
是侧棱 的中点,则异面直线
的中点,则异面直线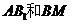 所成的角的大小是
。
所成的角的大小是
。
[答案]90°
[解析]作BC的中点N,连接AN,则AN⊥平面BCC1B1,
连接B1N,则B1N是AB1在平面BCC1B1的射影,
∵B1N⊥BM,∴AB1⊥BM.即异面直线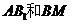 所成的角的大小是90°
所成的角的大小是90°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com