
6.(2008湖南卷7)设D、E、F分别是△ABC的三边BC、CA、AB上的点,且

 则
则 与
与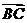 ( )
( )
A.反向平行 B.同向平行
C.互相垂直 D.既不平行也不垂直
解析: 由定比分点的向量式得:
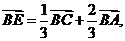
 以上三式相加得
以上三式相加得
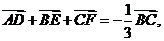 所以选A.
所以选A.
5.(2009浙江卷理)设向量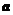 ,
, 满足:
满足: ,
, ,
,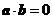 .以
.以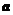 ,
, ,
, 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为 的圆的公共点个数最多为
( )
的圆的公共点个数最多为
( )
A. B.
B.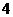 C.
C.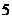 D.
D.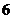
答案:C
[解析]对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有 三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
4.(2008安徽卷3).在平行四边形ABCD中,AC为一条对角线,若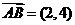 ,
,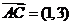 ,则
,则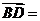 ( )
( )
A.(-2,-4) B.(-3,-5) C.(3,5) D.(2,4)
解析:因为 ,选B。
,选B。
3.(2009广东卷理)一质点受到平面上的三个力 (单位:牛顿)的作用而处于平衡状态.已知
(单位:牛顿)的作用而处于平衡状态.已知 ,
, 成
成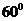 角,且
角,且 ,
, 的大小分别为2和4,则
的大小分别为2和4,则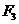 的大小为
的大小为
A. 6 B. 2 C.  D.
D. 
[解析]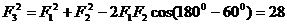 ,所以
,所以 ,选D.
,选D.
2.(2008全国一3)在 中,
中, ,
,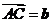 .若点
.若点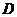 满足
满足 ,则
,则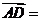 ( )
( )
A. B.
B. C.
C. D.
D.
解析:A. 由 ,
,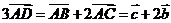 ,
, ;
;
1.(2009年广东卷文)已知平面向量a= ,b=
,b=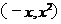 , 则向量
, 则向量
A平行于 轴
B.平行于第一、三象限的角平分线
轴
B.平行于第一、三象限的角平分线
C.平行于 轴
D.平行于第二、四象限的角平分线
轴
D.平行于第二、四象限的角平分线
[答案]
[解析]
 ,由
,由 及向量的性质可知,C正确.
及向量的性质可知,C正确.
4.电视台举办猜奖活动,参与者需先后回答两道选择题:问题A有四个选项,问题B有六个选项,但都只有一个选项是正确的。正确回答问题A可获奖金m元,正确回答问题B可获奖金n元。
活动规定:①参与者可任意选择回答问题的顺序;②如果第一个问题回答错误,则该参与者猜奖活动中止。
一个参与者在回答问题前,对这两个问题都很陌生,因而准备靠随机猜测回答问题。试确定回答问题的顺序使获奖金额的期望值较大。
3.如图所示,在三棱锥P-ABC中,PA⊥平面ABC, , E为AC的中点。
, E为AC的中点。
(1)求异面直线BE与PC所成角的余弦值;
(2)求二面角P-BE-C的平面角的余弦值。

2.(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。
(1)化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点 到直线
到直线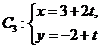 (t为参数)距离的最小值。
(t为参数)距离的最小值。
1.(本小题满分10分)选修4-2 矩阵与变换.
已知二阶矩阵M满足 ,求
,求
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com