
1.化学与生活、社会密切相关。下列说法不正确的是( )
A.利用太阳能等清洁能源代替化石燃料,有利于节约资源、保护环境
B.凡含有食品添加剂的食物对人体健康均有害,不可食用
C.为防止电池中的重金属等污染土壤和水体,应积极开发废电池的综合利用技术
D.提倡人们购物时不用塑料袋,是为了防止白色污染
23.(1)证明:连接 交
交 于
于 点,连接
点,连接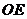 ,
,
因为底面是菱形,得 点为
点为 的中点,
的中点,
所以 ,而
,而 平面
平面 ,
,
得 平面
平面 ,而
,而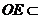 平面
平面 ,
,
所以平面 ⊥平面
⊥平面 ;
;

(2)解:连接 交
交 于
于 点,引
点,引 与
与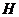 点,连结
点,连结 ,由于
,由于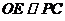 ,
, ,可得
,可得 ,故
,故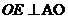 ,又因为
,又因为 ,
,
故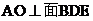 ,
, 为所求二面角的平面角.
为所求二面角的平面角.
因为  ,
,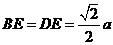 ,
,
故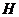 为
为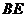 中点,
中点, ,故
,故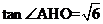 ,
,
所以二面角为 .
.
李传牛老师自2001年4月-----现在,一直连续担任海南省边防总队教导大队文补队公安边消警院校招生统考数学教员,对于数学统考试卷的出题特点有着深刻的把握,在教学和资料编辑中,注重解题过程的展示,针对2009年(2010年也使用该套书)新数学课本,每道题目包括选择和填空李老师都写好详细解析,并命制了模拟试卷十套,望有需要着联系。
另外针对部分考生基础比较薄弱的特点,我根据重要的知识点编辑了系列基础训练题,突破基础才能够更好理解应用数学概念。
联络方式:手机:13976611338 QQ :284682392
23.如图所示,已知四棱锥 的底面是边长为
的底面是边长为 的菱形,
的菱形, ,
,
 平面
平面 ,
, ,
,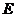 为
为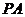 的中点.
的中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求二面角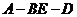 的大小.
的大小.

22.(1)解:设直线 ,即
,即 ,
,
再设 ,联合直线方程与双曲线方程
,联合直线方程与双曲线方程
得 ,
,
整理得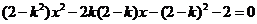 ,
,
而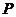 为
为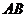 中点,则
中点,则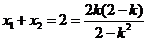 ,
,
得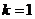 ,
,
所以直线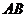 的方程为
的方程为 .
.
(2)证明:设过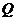 的直线为
的直线为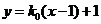 ,
,
代入双曲线得 ,
,
整理得 ,
,
若存在以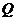 为中点的弦,则设弦的端点的横坐标为
为中点的弦,则设弦的端点的横坐标为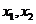 ,
,
则 ,得
,得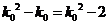 ,即
,即 ,
,
 ,
,
所以不存在以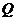 为中点的弦.
为中点的弦.
22.(课本题)已知双曲线 与点
与点 ,过
,过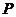 点作直线
点作直线 与双曲线交于
与双曲线交于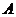 、
、
两点,若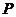 为
为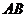 中点.
中点.
(1)求直线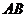 的方程;
的方程;
(2)若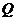 点坐标为
点坐标为 ,证明不存在以
,证明不存在以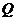 为中点的弦.
为中点的弦.
22.解:设直线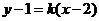 ,再设
,再设 ,
,
而点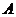 、
、 在双曲线上,则
在双曲线上,则 ,且
,且 ,
,
相减得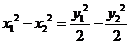 ,即
,即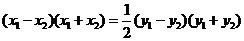
而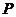 为
为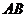 中点,则
中点,则 ,
,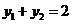 ,
,
即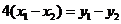 ,得
,得 ,
,
所以直线 的方程为
的方程为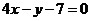 .
.
22.已知双曲线 与点
与点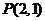 ,过
,过 点作直线
点作直线 与双曲线交于
与双曲线交于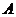 、
、 两点,
两点,
若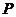 为
为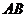 中点,求直线
中点,求直线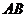 的方程.
的方程.
21.(1)解: ,
,
而 ,得
,得 ,
,
即 ,得
,得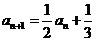 ;
;
(2)证明:由(1)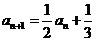 ,
,
得 ,
,
所以 是等比数列;
是等比数列;
(3)当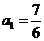 时,
时, 是以
是以 为首项,以
为首项,以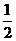 为公比的等比数列,
为公比的等比数列,
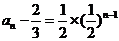 ,得
,得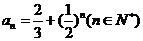 .
.
21.(课本题)设二次方程 有两个实根
有两个实根 和
和 ,
,
且满足 .
.
(1)试用 表示
表示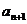 ;
;
(2)求证: 是等比数列;
是等比数列;
(3)当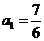 时,求数列
时,求数列 的通项公式.
的通项公式.
21.(1)解: ,
,
而 ,得
,得 ,
,
即 ,得
,得 ;
;
(2)证明:由(1) ,
,
得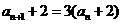 ,
,
所以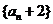 是等比数列;
是等比数列;
(3)当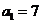 时,
时,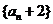 是以
是以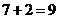 为首项,以
为首项,以 为公比的等比数列,
为公比的等比数列,
 ,得
,得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com