
新课改在教育理念、课程目标、课程内容、教学方法上作出了很大的改进,那么我作为数学教师,该如何面对数学--这个相对来说枯燥的基础学科呢?怎么去看待学生--这些未来的栋梁之才呢?怎么去对待课堂--我们自身实现价值的所在地呢?
在这一年中,我感慨很多,因为通过新课改,我真实的感受到了自己和学生的变化,对数学的理解加深了很多,我和学生一起体会到了数学带来的快乐。
数学不只是数学符号的组合,她具有更丰富的内涵,数学本来源于生活,生活也需要数学。为了使学生体会到生活与数学的紧密相关,我做了一次实验:让全班同学在一天之中不使用数学知识,看能否度过,结果基本没有同学完成。简单的:打电话,买各种东西需要数字;复杂的:去某处,需要打听其具体的方位;两个商场,一个买100赠50现金券,另一个全场6折,哪个便宜;参加抽奖,中的概率有多大等等。这一年中,我经常在课堂上引用生活上的例子来建立数学模型,通过这种途径调动学生的积极性,取得很好的效果,也没有谁来找我说数学没用了。数学教育的目的不是让学生会做各种各样的题形,而是让学生了解到数学作为一门基础学科的社会价值,进而体会一种数学思想。
能够得到上述的效果是有一个前提的,就是创设轻松愉快的学习环境,我个人认为,师生关系的融洽是即或学生情感、提高教学质量的一个重要方面。首先让学生接受你,喜欢你,才能在你的课堂上认真听讲,其次,你讲的东西必须有意思,有内容,学生才能听进去,听得懂,否则,他再和你好,再听你的话,也只能做到上你的课不说话,不添乱,给你面子而已。这些在以前的课程标准中也有要求,但是所言不详,新课改要求我们必须课前列出本节课的提纲,课后进行每节反思,这样,在上课时我的知识脉络十分清楚,奇思妙语信手拈来,生活例子旁征博引,我的课自然就成为了学生的最爱。每节课后都进行反思,这对于我们这些年轻教师非常重要,只有能及时找到自己的不足,下节课才能作到有的放矢,不犯错误。
提高了学生学习数学的兴趣,让学生们体会了数学在生活中的价值,最终的目的还是为高考服务,也就是最后还得落实到分上。有了学习兴趣,对数学的理解加深了,数学自然也就不难了,这时只要对学生的方法稍加点拨,成绩也就上来了。
除了必要的课堂教学以外,更多的是要求学生进行归纳,总结,反思。这个环节更多的让他们组队学习,与其我讲,不如他们自己讲;与其别人给他讲,不如自己悟,这个道理我的学生已经学会了,因此,目前的课堂教学,我非常轻松,课堂上轻松,自然,但是不杂乱。
以上是我在新课改这一年的实践经历,也是我的一点心得和体会。
而且数学教育存在误区,为了迎合高考,不得以培养了一批批只会做题的考试机器,做大量的、重复的习题,会学习的孩子知道归纳、总结,可以少走弯路,可是这种能力更多的孩子不具有,他们只是处于无聊的,不得不学的状态,这样他们对数学的理解还剩下多少?因此,对于他们来说,数学很无聊,数学很可怕,数学很讨厌……这当然不是我们学习数学的初衷。
4、上海师范大学,黎加厚《现代教育技术对基础教育课程改革的影响》。
3、全日制普通高级中学教科书(试行修订本·必修),2000.11。
2、1983年,中国数学会、北京师范大学编《数学通报》第4期。
受新知识体系的影响,作为最近一个世纪才兴起的“向量数学”这套数学体系,以其优良的运算通性,将数学中的“数量”运算与物理中的“矢量”运算有机地结合起来,充分数学作为一门基础性学科的重要地位。
向量作为一种新的量,它不同于数量,数量的代数运算在向量范围不一定能施行,因此在实际教学中,应明确数量和向量的区别,并重新规定了向量的加法、减法、实数和向量的积、向量的数性积和矢性积等运算法则。并在引入二维坐标系后,将向量与坐标紧紧联系起来,增加了向量的渗透性和实用性,更体现了向量运算的价值,下面简单附几例以亨读者。
例1
设△ABC是锐角三角形,在△ABC外分别作等腰Rt△BCD、△ABE、△CAF,在这三个三角形中,∠BDC、∠BAE、∠CFA是直角,又在四边形BCFE外作等腰Rt△EFG,∠EFG是直角,求证:(1)GA= AD (2)∠GAD=1350
AD (2)∠GAD=1350
(1994年上海市试题)
|
 [简析]:以点A为原点建立直角坐标系(复平面),记G相应的复数为ZG,D相应复数为ZD,如图,
[简析]:以点A为原点建立直角坐标系(复平面),记G相应的复数为ZG,D相应复数为ZD,如图,
 ZG=AG=AF+FG
ZG=AG=AF+FG
|
|
 =AF+EF
=AF+EF
|
|













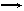
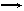
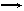
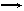



 =AF(1+
=AF(1+ )+BA
)+BA
|
|
 (-1+
(-1+ )ZD=(-1+
)ZD=(-1+ )AD
)AD
=DA+AD







 =DB+BA+(AC+CD)
=DB+BA+(AC+CD)
=BA+DB+BD+AC
=BA+(AF+FC)
=BA+AF(1+ )
)
∴ZG=(-1+ )ZD 即 GA=
)ZD 即 GA= AD ,∠GAD=1350 。
AD ,∠GAD=1350 。
[评析]:此题将向量与复数二维坐标系完美地结合起来,化繁为简,创造性使用向量完成了证明,值得同学们借鉴。本题也可用传统平几证明方法证明,这里不再赘述。
例2 如图,已知位于同一平面内的正三角形ABC,CDE和EHK(顶点依逆时针方向排列),并且AD=DK。证明:△BHD也是正三角形。
|
|
|
|
|



 [简析]:将△CAD绕C点逆时针旋转600,易知其得到△CBE, ∴ │AD│=│BE│ 且AD、BE夹角为600
又∵AD=DK
[简析]:将△CAD绕C点逆时针旋转600,易知其得到△CBE, ∴ │AD│=│BE│ 且AD、BE夹角为600
又∵AD=DK











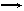
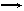

 ∴│DK│=│AD│=│BE│ 且DK、BE的夹
∴│DK│=│AD│=│BE│ 且DK、BE的夹
 角也是600
角也是600
|
|
△EHK是正三角形,所以点E转到K,线段EB
与KD重合,即B转到D



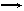
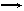

 于是│HB│=│HD│,∴HB、HD夹角为600
于是│HB│=│HD│,∴HB、HD夹角为600
∴ △BHD是正三角形。
[评析]:此题巧妙利用了向量与向量的夹角证明了正三角形的结论。实际题中条件“”等价于“在一直线上,”这个条件,读者可以利用初等平几知识进行证明,但均不如向量证法简洁明了。
|
 例3
在半径为15cm的均匀铁板上,挖去一个圆洞,已知圆洞的圆心和铁板的中心相距8cm,圆洞的半径是5cm,求挖去圆洞后所剩下的铁板的重心。
例3
在半径为15cm的均匀铁板上,挖去一个圆洞,已知圆洞的圆心和铁板的中心相距8cm,圆洞的半径是5cm,求挖去圆洞后所剩下的铁板的重心。

|
 [简析]:如图,以铁板中心O1为原点建立直角坐标系,设挖去圆洞后所剩下的铁板的重心为
[简析]:如图,以铁板中心O1为原点建立直角坐标系,设挖去圆洞后所剩下的铁板的重心为
O’(x,0)及圆洞中心O2
|
|
|
|




 如果在O’(x,0)处给一个支持点,根据重心原理,剩下的铁板应该处于力的平衡状态,即其余各力的力矩和应为0 ,则
如果在O’(x,0)处给一个支持点,根据重心原理,剩下的铁板应该处于力的平衡状态,即其余各力的力矩和应为0 ,则
|

 │F1│·│O’ O1│-│F2│·│O’ O2│=│0│
│F1│·│O’ O1│-│F2│·│O’ O2│=│0│
----------------------------------------------------------(*)
这里,│F1│=π×152 │F2│=π×52
│O’ O1│= x │O’ O2│= 8+x
代入(*)得,x = -1
∴挖去圆洞后所剩下的铁板的重心为O’(-1,0)
[评析]:这实质上是一道物理题的“变题”,利用“物体在平衡时,力矩和为0”来解题,这里力矩就一个向量,正体现了数学作为一门“工具性学科”的基础用途。
高中新教材在引入向量以后,使得平面几何和空间几何中许多定理、公式及一些相关问题变得直观、浅显、易理解。教材还通过布置一定量的“实习作业”、“研究性课题”等实践内容让学生亲身体验数学活动的过程,提高他们的数学素养,以达到培养学生创新精神和应用能力的目的,这也是高中新教材改革之宗旨和目标。
按照英国技术预测专家詹姆斯·马丁的预测,人类的科学知识在10世纪是每50年增加1倍,在20世纪中期是每10年增加1倍,而当前是每3-5年增加1倍。他的预测的精确程度还有待考究,但据联合国教科文组织的统计,截止1980年,当代人类知识体系中,人类有史以来100多万年积累的知识占10%,而近30年积累的占90%,而90年代后,人类知识积累速度更加迅速。显然人类新知识体系显现出了前所未有的高度膨胀的短周期效应, 这就使人类基础教育课程结构改革必须跟上时代发展的步伐。
现代电子办公一体化的形成,复印机、传真机、可视电话、移动通信、国际互联网(Internet)以及全球卫星定位系统可谓是真正进入了人们的日常生活。比如,网络时代的产物:E-mail的接发、信息查询(Archie)、登录环球各信息网站(www)等等,这些都标志着的高度信息化社会的到来,大量有用的和无用的信息越来越多,传播越来越便捷,人们获取和传播信息的方式和能力显然与过去有了天地之别,这对现代中学基础教课程教材提供了众多新的课题。
由于刚过去的20世纪,我国教育从中小学到大学基本了停留在18、19世纪的旧知识体系上,不少陈旧知识占去了学生相当多的学习时间,学习知识老化与迅速发展的科学技术极不相称。更加让学子们不能接受的事实是,现在所学的内容在今后5-6年毕业后,已经陈旧甚至被淘汰。怎样解决这一系列矛盾呢?现代化的电子媒介技术为基础教育课程改革提供了的新的广阔前景,这也许就是人们通常所认为的“教学相长”吧,教育推动了科学技术的进步,同样进步了的科学技术反过来又会推动教育向更高层面上发展。
在现代教育技术支持下,教师一改过去“单一的传授教材知识”转变为“辅以现代媒体技术的现代教材体系”。 目前,新的课程数学教学要求中,明确增加通过“研究性课题”使学生学会提出问题,明确探究方向,体验数学活动的过程,培养创新精神和应用能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com