5、直线平行的条件的应用；

4、垂线、垂线段、线段的垂直平分线的定义及性质；

3、对顶角、余角、补角的性质及计算；度、分、秒的换算；

2、角的概念、分类及计算；

1、、线段的和与差及线段的中点；

11、掌握圆柱、圆锥的侧面积和全面积计算。

中考将继续考查圆的有关性质，其中圆与三角形相似(全等)。三角函数的小综合题为考查重点；直线和圆的关系作为考查重点，其中直线和圆的位置关系的开放题、探究题是考查重点；继续考查圆与圆的位置五种关系。对弧长、扇形面积计算以及圆柱、圆锥的侧面积和全面积的计算是考查的重点。

应试对策

圆的综合题，除了考切线、弦切角必须的问题。一般圆主要和前面的相似三角形，和前面大的知识点接触。就是说几何所有的东西都是通的，你学后面的就自然牵扯到前面的，前面的忘掉了，简单的东西忘掉了，后面要用就不会用了，所以几何前面学到的知识、常用知识，后面随时都在用。直线和圆以前的部分是重点内容，后面扇形的面积、圆锥、圆柱的侧面积，这些都是必考的，后面都是一些填空题和选择题，对于扇形面积公式、圆锥、圆柱的侧面积的公式记住了就可以了。圆这一章，特别是有关圆的性质这两个单元，重要的概念、定理先掌握了，你首先要掌握这些，题目就是定理的简单应用，所以概念和定理没有掌握就谈不到应用，所以你首先应该掌握。掌握之后，再掌握一些这两章的解题思路和解题方法就可以了。你说你已经把一些这个单元的基本定理都掌握了，那么我可以在这里面介绍一些掌握的解题思路，这样你把这些都掌握了，解决一些中等难题。都是哪些思路呢？我暂认为你基本知识掌握了，那么，在圆的有关性质这一章，你需要掌握哪些解题思路、解题方法呢？第一，这两章有三条常用辅助线，一章是圆心距，第二章是直径圆周角，第三条是切线径，就是连接圆心和切点的，或者是连接圆周角的距离，这是一条常用的辅助线。有几个分析题目的思路，在圆中有一个非常重要，就是弧、常与圆周角互相转换，那么怎么去应用，就根据题目条件而定。

例题精讲

例1、如图，A、B、C、D是⊙O上的三点，∠BAC=30°，则∠BOC的大小是　 (　　　 )

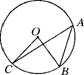A、60°　　 B、45°　　　 C、30°　　　 D、15°

答案：A

例2.一如图，方格纸上一圆经过(2，5)、(-2，2)、(2，-3，)、(6，2)四点，则该圆圆心的坐标为　　　　 (　　 )

　 A．(2，-1)　　 B．(2，2)　　 C．(2，1)　　 D．(3，1)

答案：C

例3.已知⊙O的半径为10 cm，如果一条直线和圆心O的距离为10 cm,那么这条直线和这个圆的位置关系为(　　 )

A相离　　 B.相切　　 C．相交　　 D．相交或相离

答案：B

例4.已知：如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=130°，过D点的切线PD与直线AB交于P点，则∠ADP的度数为(　 )

　 A．40°　　 B．45°　　 C．50°　 D．65°

答案：A

例5.如图，以O为圆心的两个同心圆的半径分别为11cm和9 cm，若⊙P与这两个圆都相切，则下列说法中正确的是(　　 )．

　　 (A)⊙P的半径可以为2cm

　　 (B)⊙P的半径可以为10 cm

　　 (C)符合条件的④P有无数个且P点运动的路线是曲线

(D)符合条件的⊙P有无数个且P点运动的路线是直线

答案：B、C

例6、如图4，⊙O的半径为5cm，圆心到弦AB的距离为3cm，则弦AB的长为_____________________cm；

答案：8

例7：边长为6的正六边形外接圆半径是___________________；

答案：6

例8.如图，三个同心扇形的圆心角∠AOB为120°，半径OA为6 cm，C、D是︵AB的三等分点，则阴影部分的面积等于　　　　 cm²．

答案：4π

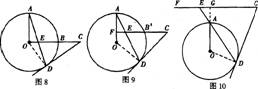
例9.(1)如图8，OA、OB是⊙O的两条半径，且OA⊥OB，点C是OB延长线上任意一点：过点C作CD切⊙O于点D，连结AD交DC于点E．求证：CD=CE　　

(2)若将图8中的半径OB所在直线向上平行移动交OA于F，交⊙O于B’，其他条件不变(如图9)，那么上述结论CD=CE还成立吗?为什么?

(3)若将图8中的半径OB所在直线向上平行移动到⊙O外的CF，点E是DA的延长线与CF的交点，其他条件不变(如图10)，那么上述结论CD=CE还成立吗?为什么

分析：本题主要考查圆的有关知识，考查图形运动变化中的探究能力及推理能力．

　 解答：(1)证明：连结OD　 则OD⊥CD，∴∠CDE+∠ODA=90°

　 在Rt△AOE中，∠AEO+∠A=90°

　 在⊙O中，OA=OD∴∠A=∠ODA，　　 ∴∠CDE=∠AEO　　

　 又∵∠AEO=∠CED，∠CDE=∠CED　　 ∴CD=CE

　 (2)CE=CD仍然成立．　　

　 ∵原来的半径OB所在直线向上平行移动∴CF⊥AO于F，

　 在Rt△AFE中，∠A+∠AEF=90°．

　 连结OD，有∠ODA+∠CDE=90°，且OA=OD ．∠A=∠ODA

　 ∴∠AEF=∠CDE 　又∠AEF=∠CED　　 ∴∠CED=∠CDE∴CD=CE

　 (3)CE=CD仍然成立．

　 ∵原来的半径OB所在直线向上平行移动．AO⊥CF

　 延长OA交CF于G，在Rt△AEG中，∠AEG+∠GAE=90°

　 连结OD，有∠CDA+∠ODA=90°，且OA=OD∴∠ADO=∠OAD=∠GAE

∴∠CDE=∠CED　　 ∴CD=CE

例10.如图1，已知AB是⊙O的直径，AB垂直于弦CD，垂足为M，弦AE与CD交于F，则有结论AD²=AE·AF成立(不要求证明)．

　　 (1)若将弦CD向下平移至与⊙O相切于B点时，如图2，则AE．AF是否等于AG²?如果不相等，请探求AE·AF等于哪两条线段的积?并给出证明．　　

　　 (2)当CD继续向下平移至与⊙O相离时，如图3，在(1)中探求的结论是否还成立，并说明理由

(1)

解：A E·AF不等于AG²，应该有结论AE·AF=AG·AH．证明：连结BG，EG．∴AB是⊙O的直径，CD是⊙O的切线，∴∠ABF=∠AGB=90°，∠BAF+∠BFA=90°，∴∠AGE+∠BGE=90°，∴∠BAF+

∠BFA=∠AGE+∠BGE，而∠BAF=∠BGE，∠BFA=∠AGE，又∠FAH=∠GAE，∴△FAH∽△GAE，．AE·AF=AG·AH；　 (2)①中探求的结论还成立．证明：连结EG，BG，AB是⊙O的直径，AM⊥CD，∴∠AMF=∠AGB=90°，∴∠AFM+∠FAM=∠AGE+∠BGE=90°，而∠FAM=∠BGE，∴∠AFM=∠AGE，又∠FAH=∠GAE，△FAH∽△GAE，∴A E·A F=AG·A H．　

例11.已知半径为R的⊙O’经过半径为r的⊙O的圆心，⊙O与⊙O'交于E、F两点．　

(1)如图(1)，连结00'交⊙O于点C，并延长交⊙O’于点D，过点C作⊙O的切线交⊙O’于A、B两点，求OA·OB的值；　　

(2)若点C为⊙O上一动点，①当点C运动到⊙O’时，如图(2)，过点C作⊙O的切线交⊙O'，于A、B两点，则OA·OB的值与(1)中的结论相比较有无变化?请说明理由．

②当点C运动到⊙O'外时，过点C作⊙O的切线，若能交⊙O'于A、B两点，如图(3)，则OA·OB的值与(1)中的结论相比较有无变化?请说明理由．

解。(1)连结DB，则∠DBO=90°

　　 ∵AB切⊙O于点C∵．AB⊥OD，又OD是⊙O’直径，即OA=OB

　　 得OA²=OC·OD=r·2R=2Rr．即OA·OB=2rR

　　 (也可证明△OBD∽△OCA)

　　 (2)无变化　 连结00'，并延长交⊙O'于D点，连结DB、OC．

　　 证明△OCA∽△OBD，得OA·OB=OC·OD=r·2R=2Rr

　　 (3)无变化　 连结00’，并延长交⊙O’于B点，连结DB、OC

　　 证出△OCA∽△OBD，得OA·OB=OC·OD．：r·2R=2Rr

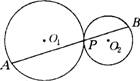
例12已知：如图1，⊙O₁与⊙O内切于P点，过P点作直线⊙O₁于A点，交⊙O₂于B点，C为⊙O₁上一点，过B点作⊙O₂的切线交直线AC于Q点．

(1)求证：AC·AQ=AP·AB；

(2)若将两圆内切改为外切，如图2，其他条件不变，(1)中的结论是否仍然成立?请你画出图形，并证明你的结论．

解答：(1)证明：过点P作⊙01、⊙O₂的外公切线PT，连PC．(如图)则∠3=∠C

　∵BQ为0Q的切线，∴∠1=∠3．∴∠1=∠C．

　 又∵∠1=∠2，∴∠2=∠C．

　 △ABQ∽△ACP

　 ∴AC·AQ=AP·AB．

　 (2)答：(1)中的结论仍然成立，(如图14)

　 证明：过点P作⊙O₁、⊙O₂的内公切线PT． 则∠3=∠4．

　 ∵BQ为⊙O₂的切线，∴∠1=∠2．

　 又∵∠2=∠3，∴∠1=∠4．

　 ∴△APC∽△AQB∴．AP/AC=AQ/AB

∴AP·AB=AC·AQ．

10、理解圆柱、圆锥的侧面展开图。

9、掌握弧长、扇形面积计算公式。

8、两圆的位置关系与两个圆半径的和或差与圆心距之间的关系式。两圆相切、相交的性质。

7、圆和圆的五种位置关系。