1、理解锐角三角形函数角的三角函数的值；

3、掌握用扇形统计图表示数据，计算加权平均数，根据具体问题可选择合适 的统计图表示数据 的集中程度；计算极差和方差，并用它们表示数据的离散程度。列频率分布表，画频数分布直方图和频数折线图，并解决简单的实际问题；样本估计总体的思想，用样板的平均数、方差估计总体的平均数。方差，根据统计结果作出合理的判断和预测，比较清晰的表示自己的观点，对日常生活中的某些数据发表自己的看法，认识到统计在社会生活及科学领域中应用，并能解决一些简单的实际问题。

中考将继续考查总体、样本及样本容量等概念，以及确定平均数、众数、中位数、标准差。

应试对策

1牢固掌握概念，并能掌握概念间的区别和联系，以及在实际问题中应用。

2统计的特点是与数据打交道解题时计算较繁，所以要有意识培养认真、耐心、细致的学习态度和学习习惯。

3要关注统计知识与方程、不等式相结合的综合性试题，会读频率分布直方图，会分析图表，注重能力的培养、加大训练力度。

例题精讲

今年我市初中毕业生人数为12．8万人，比去年增加了9%，预计明年初中毕业生人数将比今年减少9%，下列说法：①去年我市初中毕业生人数约为万人；②按预计，明年我市初中毕业生人数将与去年持平；③按预计，明年我市初中毕业生人数会比去年多．其中正确的是(　　 )

　A①②　 B①③　 C.②③　 D．①　　　　　

答案：D

在样本方差的计算式S²=(x₁-20)²+(x₂-20)²+…+(x₁₀-20)²]中，数字10与20分别表示样本的　　 (　　 )

　 A．容量、方差　　 B．平均数、容量

　 C．容量、平均数　　 D．标准差、平均数

答案：C

下表是某校初三(1)班20名学生某次数学测验的成绩统计表

　　 (1)若这20名学生成绩的平均分数为82分，求x和y的值；

(2)在(1)的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值．

解：根据题意，得1+5+x+y+2=20　 60+70×5+80x+90y+100 2=8220 ，解得x=5 y=7　 (2)a=90 b=80

已知一组数据：6，3，4，7，6，3，5，6

　 (1)求这组数据的平均数、众数、中位数；

　 (2)求这组数据的方差和标准差．

解：(1)按从小到大的顺序排列数据：3，3，4，5，6，6，6，7．　　

　 平均数5　 众数是6，中位数是5．5

　 (2)方差=2 标准差s=

为了调查不同面额纸币上细菌数量与使用频率之间的关系．某中学研究性学习小组从银行、商店、农贸币场及医院收费处随机采集了 8种面额的纸币各30张，分别用无菌生理盐水漂洗这些纸币，对洗出液进行细菌培养，测得数据如下表．

(1)计算出被采集的所有纸币平均每张的细菌个数约为　　　　 (结果取整数)．(2)由表中数据推断出面额为　　　　 的纸币的使用频率较高．根据上面的推断和生活常识总结出：纸币上细菌越多，纸币的使用频率　　　　 ．看来，接触钱币以后要注意洗手噢!

答案：(1)5417(2)l元，越高

小谢家买了一辆小轿车，小谢连续记录了七天每天行驶的路程．

请你用统计初步的知识，解答下列问题：(1)小谢家小轿车每月(每月按30天计算)要行驶多少千米?(2)若每行驶100千米需汽油8升，汽油每升3．45元．请你求出小谢家一年(一年按12个月计算)的汽油费是多少元?

解：(1)由图知这七天中平均每天行驶的路程为50(千米)．

∴每月行驶的路程为30×50=l 500(千米)．

答：小谢家小轿车每月要行驶1500千米．

(2)小谢一家一年的汽油费用是4 968元．

2、理解 频数、频率的概念

1、了解总体、个体、样本不同的抽样可能得到不同的结果，频数分布的意义和作用，

6.感受图形变化后的坐标的变化

例题精讲

例1.三角形的两条边长分别为3cm和4cm，第三边的长度量数是奇数，那么这个三角

是形的周长　　　　　　　　 (　 )B

A、8cm或10cm　　　 B、10cm或12cm　

C、12cm或14cm　　　 D、12cm

答案：B

例2.如图8，在△ABC中，AB=AC，∠A=36°，BD、CE分别

为∠ABC与∠ACB的角平分线，且相交于点F，则图中

的等腰三角形有　　　　　　 (　 )C

A、6个　　　 B、7个　　　 C、8个　　　 D、9个

答案：C

例3.已知：如图9，△ABC中，P为AB上的一点，在下列四

个条件中： ① ∠ACP=∠B　 ② ∠APC=∠ACB　

③ AC²=AP·AB　 ④ AB·CP=AP·CB，能满足△APC和

△ACB相似的条件是　　　　 (　 )D

A、①②④　 B、①③④　 C、②③④　 D、①②③

答案：D

例4.如图7，在正方形网格上有6个三角形

①　　 △ABC，② △BCD，③ △BDE，

④ △BFG，⑤ △FGH，⑥ △EFK，其中

②-⑥中与三角形①相似的是 (　 )B

A、②③④　　　　　 B、③④⑤

C、④⑤⑥　　　　　 D、②③⑥

答案：B

　　　　　　　　　 图7

例5.如图，在．△ABC中，AC>AB，点D在AC边上(点D不与A、C重合)，若再增加一个条件就能使△ABD∽△ACB，则这个条件可以是　　　　

答案：∠ABD=∠C或∠ADB=∠ABC　 AD/AB=AB/AC

例6.如图，正方形ABCD边长是2，BE=CE，MN=1，线段MN的两端在CD、AD上滑动，当DM=　　　　 时，△ABE与以D、M、N为顶点的三角形相似．

答案：/5或2/5

例7. 如图3，在△ABC中，如果AB=30cm，BC=24cm，

CA=27cm，AE=EF=FB，EG∥DF∥BC，FM∥EN∥AC，

图中阴影部分的三个三角形周长的和为　　　 cm；

答案：81；

例8.在△ABC中AB=AC，AB的中垂线与AC所在直线相

交所得的锐角为50°，则底角B的大小为　　　　 。

答案：70°或20°

例9. 如图，以等腰直角三角形ABC的斜边AB为边向内作等边三角形ADB，连结DC，

　 以DC为边作等边三角形DCE，B、E在C、D的同侧，若AB=，求：BE的值。

. 解：∵∠ADC=60°－∠BDC，∠BDE=60°－∠BDC，

∴∠ADC=∠BDE，

再由AD=BD，CD=ED，∴△ADC≌△BDE

∴AC=BE，在等腰三角形ABC中，AB=，∴AC=1，即BE=1

例10. 如图，△ACB、△ECD都是等腰直角三角形，且C在AD上，AE的延长线与BD交

于F， 　 请你在图中找出一对全等三角形，并写出证明它们全等的过程。

解：△ACE≌△BCD；证明过程如下：

∵△ACB、△ECD都是等腰直角三角形

∴AC=BC，∠ACE=∠BCD=90°，CE=CD

∴△ACE≌△BCD

例 　 11. 如图，已知：AD=AE，DF=EF；求证：△ADC≌△AEB

证明：连结AF　 AD=AE　 DF=EF　　　　 △ADF≌△AEF

　　　　　　　　　　　 AF=AF

∠ADC = ∠AEB

AD=AE　　　　 △ADC≌△AEB

∠DAC = ∠EAB　　

例12. 如图，F、C是线段BE上的两点，BF=CE，AB=DE，∠B=∠E，QR∥BE；

求证：△PQR是等腰三角形

　 证明：∵ BF=CE　　　 ∴ BC=EF

又∵ ∠B=∠E，AB=DE　　 ∴ △ABC≌△DEF

∴ ∠ACB=∠DEF

又∵ QR∥BE　　　　　　 ∴ ∠ACB=∠Q，∠DFE=∠R

∴ ∠Q=∠R　　　　　　 ∴ △PQR是等腰三角形

例13. 如图，在△ABC中，∠A=90°P为AC边的中点，PD⊥BC，D为垂足；

　　　　 　 求证：BD²－CD² = AB²

证明：连结BP，在Rt△BPD中，BD²= BP²－PD² ①

在Rt△CDP中，CD²= PC²－PD² ②　

由①－② 得： BD²－CD² = BP²－PC²

　　　 ∵ AP=PC　　　 ∴ BD²－CD² = BP²－AP²

又∵ ∠A=90°　 ∴ 在Rt△ABP中，AB²= BP²－AP²

∴ BD²－CD²= AB²

例14. 如图，梯形ABCD中，AB∥CD，E为DC中点，直线BE交AC于F，交AD的延长

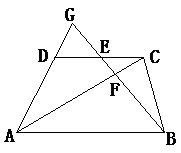　 　 线于G；求证：EF·BG=BF·EG

证明：∵ AB∥DC　 ∴ △EFC∽△BFA，△GDE∽△GAB

∴ EF/BF = EC/AB， EG/BG = DE/AB

又∵ DE = EC 　　∴ EC/AB = DE/AB

∴ EF/BF = EG/BG　 即EF·BG = BF·EG

5.在坐标系描述物体的位置。

4、会画直角坐标系，会根据坐标描出点的位置，由点的位置写出它的坐标，会灵活运用不同的方式确定物体的位置，由点的位置写出它的坐标，

3、在综合题中，注意相似形的灵活运用，并熟练掌握等线段、等比代换，等代换技巧的运用，培养综合运用知识的能力；

2、运用相似形的知识解决一些实际问题，要能够在理解题意的基础上，把它转化为纯数学知识的问题，要注意培养数学建模的思想；

1、要掌握基本知识和基本技能；