
16.(本小题满分13分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点,
 PD⊥平面ABCD,且PD=AD=
PD⊥平面ABCD,且PD=AD= ,CD=1
,CD=1
(1)证明:MN∥平面PCD;
(2)证明:MC⊥BD;
(3)求二面角A-PB-D的余弦值。
15.(本小题满分13分)
已知函数 .
.
(1)求 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(2)求 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。
14.无穷等差数列 的各项均为整数,首项为
的各项均为整数,首项为 、公差为
、公差为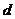 ,
, 是其前
是其前 项和,3、21、15是其中的三项,给出下列命题;
项和,3、21、15是其中的三项,给出下列命题;
①对任意满足条件的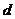 ,存在
,存在 ,使得99一定是数列
,使得99一定是数列 中的一项;
中的一项;
②对任意满足条件的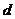 ,存在
,存在 ,使得30一定是数列
,使得30一定是数列 中的一项;
中的一项;
③存在满足条件的数列 ,使得对任意的
,使得对任意的
 N
N ,
, 成立。
成立。
其中正确命题为 。(写出所有正确命题的序号)
13.将编号为1、2、3的三个小球,放入编号为1、2、3、4的四个盒子中
如果每个盒子中最多放一个球,那么不同的放球方法有 种;
如果4号盒子中至少放两个球,那么不同的放球方法有 种。
12.在△ABC中, ,
, ,
, 分别是三个内角A,B,C的对边,若
分别是三个内角A,B,C的对边,若 ,
, ,
, ,则
,则 。
。
11.若直线 与圆
与圆 相切,则
相切,则 。
。
10. 的展开式中的常数项为
。
的展开式中的常数项为
。
9.设 是虚数单位,则
是虚数单位,则 。
。
8.若椭圆或双曲线上存在点P,使得点P到两个焦点的距离之比为2:1,则称此椭圆或双曲线存在“F点”,下列曲线中存在“F点”的是 ( )
A. B.
B.
C. D.
D.
第Ⅱ卷(非选择题,共110分)
7.已知 ,设
,设 ,
,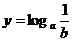 ,
, ,则 ( )
,则 ( )
A. B.
B.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com