
19.(本小题满分12分)
某社区举办2010年上海世博会知识宣传活动,进行现场抽奖,抽奖规则是:盒中装有10张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案,参加者每次从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖.
(1)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人笑说:我只知道若从盒中抽两张都不是“海宝”卡的概率是 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(2)现有甲乙丙丁四人依次抽奖,抽后放回,另一个人再抽,用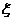 表示获奖的人数,求
表示获奖的人数,求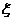 的分布列及
的分布列及 .
.
18.(本小题满分12分)
 如图,四棱锥
如图,四棱锥 的底面是矩形,
的底面是矩形,
 底面
底面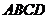 ,P为BC边的中点,SB与
,P为BC边的中点,SB与
平面ABCD所成的角为45°,且AD=2,SA=1.
(1)求证: 平面SAP;
平面SAP;
(2)求二面角A-SD-P的大小.
请把解答过程写在答题卡相应位置上.)
17.(本小题满分10分)
在△ABC中,已知角A、B、C所对的边分别是a、b、c,且a=2, ,设
,设 .
.
(1)用 表示b;
表示b;
(2)若 求
求 的值.
的值.
16.与直线 和圆
和圆 都相切的半径最小的圆的方程是
都相切的半径最小的圆的方程是
★ .
15.ABCD与CDEF是两个全等的正方形,且两个正方形所在平面互相垂直,M是BC的中点,则异面直线AM与DF所成角的正切值为 ★ .
14. 中,三内角
中,三内角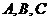 所对边的长分别为
所对边的长分别为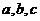 ,已知
,已知 ,不等式
,不等式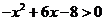 的解集为
的解集为 ,则
,则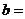 ★
.
★
.
13.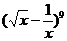 展开式中,常数项是 ★ .
展开式中,常数项是 ★ .
12.已知f (x)为偶函数,且f (2+x)=f (2-x),当-2≤x≤0时,f (x)=2x, an=f (n), n∈N*,则a2010的值为
A.2010 B.4 C.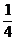 D.-4
D.-4
第Ⅱ卷(非选择题,共90分)
11.F1、F2分别是双曲线 的左、右焦点,A是其右顶点,过F2作
的左、右焦点,A是其右顶点,过F2作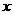 轴的垂线与双曲线的一个交点为P,G是
轴的垂线与双曲线的一个交点为P,G是 ,则双曲线的离心率是学
,则双曲线的离心率是学
A.2 B.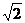 C.3 D.
C.3 D.
10.在三棱锥A-BCD中,侧棱AB、AC、AD两两垂直,△ABC、△ACD、△ADB的面积分别为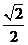 、
、 、
、 .则三棱锥A-BCD的外接球的体积为
.则三棱锥A-BCD的外接球的体积为
A. B.
B. C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com