
5、不等式 表示的平面区域在直线
表示的平面区域在直线 的( )
的( )
A.左上方 B.右上方 C.左下方 D.左下方
4、已知直线 ,直线
,直线 过点
过点 ,且
,且 到
到 的夹角为
的夹角为 ,则直线
,则直线 的方程是( )
的方程是( )
A. B.
B. C.
C. D.
D.
3、直线 同时要经过第一、第二、第四象限,则
同时要经过第一、第二、第四象限,则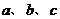 应满足( )
应满足( )
A.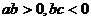 B.
B.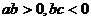 C.
C. D.
D.
2、若圆C与圆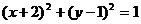 关于原点对称,则圆C的方程是( )
关于原点对称,则圆C的方程是( )
A. B.
B.
C. D.
D.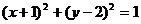
1、在直角坐标系中,直线 的倾斜角是( )
的倾斜角是( )
A. B.
B. C.
C. D.
D.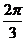
(三)解答题
14、求以达原点与圆x2+y2-4x+3=0相切的两直线为渐近线且过椭圆4x2+y2=4两焦点的双曲线方程。
15、已知P(x,y)为平面上的动点且x≥0,若P到y轴距离比到点(1,0)距离小1
(1)求点P轨迹C的方程;
(2)设过M(m,0)的直线交双曲线C于A、B两点,问是否存在这样的m,使得以线段AB为直径的圆恒过原点。
16、设抛物线y2=4ax(a>0)的焦点为A,以B(a+4,0)为圆心,|BA|为半径,在x轴上方画圆,设抛物线与半圆交于不同两点M、N,点P是MN中点
(1)求|AM|+|AN|的值;
(2)是否存在这样的实数a,恰使|AM|,|AP|,|AN|成等差数列?若存在,求出a;若不存在,说明理由。
17、设椭圆中心为0,一个焦点F(0,1),长轴和短轴长度之比为t
(1)求椭圆方程;
(2)设过原点且斜率为t的直线与椭圆在y轴右边部分交点为Q,点P在该直线上,且 ,当t变化时,求点P轨迹。
,当t变化时,求点P轨迹。
18、已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同两点A、B,|AB|≤2p,
(1)求a取值范围;
(2)若线段AB垂直平分线交x同于点N,求△NAB面积的最大值。
(二)填空题
9、已知A(4,0),B(2,2)是椭圆 内的点,M是椭圆上的动点,则|MA|+|MB|的最大值是____________。
内的点,M是椭圆上的动点,则|MA|+|MB|的最大值是____________。
10、椭圆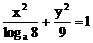 的离心率为
的离心率为 ,则a=__________。
,则a=__________。
11、高5米和3m的旗竿在水平地面上,如果把两旗竿底部的坐标分别定为A(-5,0),B(5,0),则地面上杆顶仰角相等的点的轨迹是__________。
12、若x,y∈R,且3x2+2y2=6,则x2+y2最大值是________,最小值是________。
13、抛物线y2=2x上到直线x-y+3=0距离最短的点的坐标为__________。
(一)选择题
1、方程 表示的曲线是
表示的曲线是
A、 椭圆 B、双曲线 C、抛物线 D、不能确定
2、把椭圆 绕它的左焦点顺时针方向旋转
绕它的左焦点顺时针方向旋转 ,则所得新椭圆的准线方程是 A、
,则所得新椭圆的准线方程是 A、 B、
B、
C、 D、
D、
3、方程 的曲线形状是
的曲线形状是
A、圆 B、直线 C、圆或直线 D、圆或两射线
4、F1、F2是椭圆 (a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是
(a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是
A、  B、
B、 C、
C、 D、
D、
5、若方程 表示焦点在y轴上的双曲线,则它的半焦距C的取值范围是
表示焦点在y轴上的双曲线,则它的半焦距C的取值范围是
A、(0,1) B、(1,2) C、(1,+∞) D、与m有关
6、以抛物线y2=2px(p>0)的焦半径|PF|为直径的圆与y轴位置关系是
A、相交 B、相切 C、相离 D、以上三种均有可能
7、直线y=kx-2交抛物线y2=8x于A、B两点,若AB中点横坐标为2,则|AB|为
A、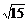 B、
B、 C、
C、 D、
D、
8、已知圆x2+y2=1,点A(1,0),△ABC内接于圆,∠BAC=600,当BC在圆上运动时,BC中点的轨迹方程是
A、x2+y2= B、x2+y2=
B、x2+y2=
C、x2+y2= D、x2+y2=
D、x2+y2=
4、圆锥曲线中参数取值范围问题通常从两个途径思考,一是建立函数,用求值域的方法求范围;二是建立不等式,通过解不等式求范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com