
(一)综合例题赏析
例11 设a、b是两条异面直线,那么下列四个命题中的假命题是( )
A.经过直线a有且只有一个平面平行于直线b
B.经过直线a有且只有一个平面垂直于直线b
C.存在分别经过直线a和b的两个互相平行的平面
D.存在分别经过直线a和b的两个互相垂直的平面
 解:B是假命题,因为对于异面直线a、b,有时不存在过直线a且垂直于直线b的平面.
解:B是假命题,因为对于异面直线a、b,有时不存在过直线a且垂直于直线b的平面.
如图,直线a是圆柱体的轴线,M、N分别为上下底圆周上的点且MN∥a,令b为直线MN,则a,b为异面直线.
过直线a的平面以直线a为轴旋转,它们均与b不垂直.
例12 已知异面直线a与b所成的角为50°,P为空间一定点,则过点P与a、b所成的角都是30°的直线有且仅有( )
 A.1条
B.2条 C.3条 D.4条
A.1条
B.2条 C.3条 D.4条
解:如图过点作PA∥a,PB∥b,则∠APB的异面直线a、b所成的平面角,由已知∠APB=50°.
作∠APB的平分线PO,任取O∈PO,作CO⊥平面APB,令CB⊥PA于A,CB⊥PB于B,则由三垂线
定理知,OA⊥PA于A,OB⊥PB于B.
考虑C点沿平面APB的垂线OC自O点出发向上移动,易知∠CPB∈(25°,90°),
∴存在唯一点C使∠CPB=∠CPA=30°.
同理在垂线CO的下方还存在对称点C′,使∠C′PA=∠C′PB.
∴符合题设的直线有且只有两条.应选B.
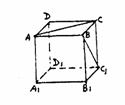 例13 如图,正方体ABCD-A1B1C1D1中,直线BC1与直线AC( )
例13 如图,正方体ABCD-A1B1C1D1中,直线BC1与直线AC( )
A.相交且垂直
B.相交但不垂直
C.异面且垂直
D.异面但不垂直
解:直线BC1和AC异面不垂直.
∵BC1∥AD1,
∴∠CAD1为异面直线AC,BC1所成的角.
在△CAD1中,CA=AD1=D1C.
∴∠CAD1=60°
即AC和BD1成60°角.
应选D.
例14 设a、b是异面直线,那么( )
A.必然存在唯一的一个平面同时平行于直线a和b
B.必然存在唯一的一个平面同时垂直于直线a和b
C.过直线a存在唯一的一个平面平行于直线b
D.过直线a存在唯一的一个平面垂直于直线b
解:A不正确.因为垂直于异面直线a、b公垂线的任何一个平面都与a、b平行.
B不正确.若a⊥α,且b⊥α,则a∥b,此与a、b异面矛盾.
C正确.
D不正确.有时过直线a的所有平面都与直线b不垂直.
∴应选C.
(十)直线与平面的综合问题
例10 如图,已知斜三棱柱ABC-A1B1C1的底面△ABC是直角三角形,∠C=90°,侧棱与底面成60°的角,点B1在底面的射影D为BC的中点,且BC=2,
(1)  求证平面AB1D⊥平面ABC.
求证平面AB1D⊥平面ABC.
(2)求证AC⊥平面BB1C1C.
(3)求证异面直线AB1与BC1垂直.
(4)如果二面角A-BB1-C的度数为30°,求四棱锥A-BB1C1C的体积.
解:(1)证明∵B1在底面上的射影为D
∴B1D⊥底面ABC,
又∵B1D AB1D,
AB1D,
∴平面AB1D⊥平面ABC.
(2)证明:由已知BC⊥AC,B1D⊥面ABC.
由三垂线定理:AC⊥B1C,AC 面ABC,故B1D⊥AC,而B1C∩B1D=B1
面ABC,故B1D⊥AC,而B1C∩B1D=B1
∴AC⊥平面B1BCC1.
(3)证明:∵BD=CD= BC=1,
BC=1,
∵侧棱与底面所成角为60°,B1D⊥底面ABC.
∴∠B1BD是侧棱与底面所成的角,∠B1BD=60°.
∴四边形BB1C1C是菱形,BC1⊥B1C
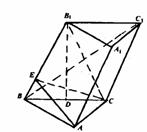 ∵B1C
∵B1C 平面BB1C1C,AC⊥平面BB1C1C
平面BB1C1C,AC⊥平面BB1C1C
∴AC⊥B1C
又B1C⊥BC1,B1C是AB1在平面BB1C1C的射影,
由三垂线定理:AB1⊥BC1.
(4)作CE⊥BB1于E,连结AE.如图1-25.
∵AC⊥面BB1C1C,
∴AC⊥CE,AC⊥BB1
∴AE⊥BB1(三垂线定理).
∴∠AEC为二面角A-BB1-C的平面角,∠AEC=30°,
在Rt△BCE中,EC=BC·sin60°=2× =
= ,
,
在Rt△ACE中,AC=CE·tg30°= ×
× =1,
=1,
∴V =
= S
S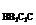 ·AC
·AC
= BB1·BC·sin60°·AC=
BB1·BC·sin60°·AC= .
.
(九)点到直线、点到平面、直线与平面、平面与平面间的距离的定义及计算
例9 已知Rt△ABC中,∠A=90°,AB=a,AC=b,沿高AD折成直二面角(如图).(1)判断此时△ABC的形状;(2)求D到平面ABC的距离.
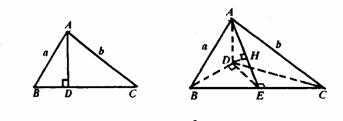 解:(1)DH⊥平面ABC,因DA、DB、DC两两互相垂直,故H为△ABC的垂心(证明略),AE⊥BC,由cosθ=cosθ1cosθ2,得cos∠ABE=cos∠ABD·cos∠DBC.
解:(1)DH⊥平面ABC,因DA、DB、DC两两互相垂直,故H为△ABC的垂心(证明略),AE⊥BC,由cosθ=cosθ1cosθ2,得cos∠ABE=cos∠ABD·cos∠DBC.
∵∠ABD和∠DBC分别为Rt△BDC的锐角,
故0<cos∠ABD,cos∠DBC<1,
∴0<cos∠ABE<1,即∠ABC为锐角,
同理可证∠ABC、∠CAB均为锐角,∴△ABC为锐角三角形.
(2)解法一:设D到平面ABC的距离为x.∵VD-ABC=VA-BDC得 xSABC=
xSABC= AD·S△BDC,
AD·S△BDC,
解出x=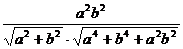 .
.
解法二:作AE⊥BC,AD⊥平面DBC,故DO⊥BC.BC⊥平面ADE,平面ADE⊥平面ABC,作DH⊥AE,则AE是D到平面ABC的距离(以点线距离代替点面距离).在Rt△ADE中,DH是斜边AE上的高,解出
DH=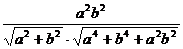 .
.
(八)二面角
例8 如图,梯形ABCD中,BA⊥AD,CD⊥AD,AB=2,CD=4,P为平面ABCD外一点,平面PAD⊥平面ABCD,△PBC是边长为10的正三角形,求平面PAD与面PBC所成的角.

 解法一:如图,延长DA、CB交于E,
解法一:如图,延长DA、CB交于E,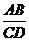 =
= =
= ,∴AB是△ECD的中位线,CB=BE=10.又△PCB为正△,易证△PCE为直角三角形,PE⊥PC.又平面PDA⊥平面ABCD,且CD⊥交线DA,∴CD⊥平面PDE.PE是PC在平面PDE内的射影,∴PE⊥PD(三垂线定理的逆定理).故∠CPD是D-PE-C的平面角.在Rt△CDP中,sin∠DPC=
,∴AB是△ECD的中位线,CB=BE=10.又△PCB为正△,易证△PCE为直角三角形,PE⊥PC.又平面PDA⊥平面ABCD,且CD⊥交线DA,∴CD⊥平面PDE.PE是PC在平面PDE内的射影,∴PE⊥PD(三垂线定理的逆定理).故∠CPD是D-PE-C的平面角.在Rt△CDP中,sin∠DPC= =
= ,故二面角大小为arcsin
,故二面角大小为arcsin .
.
 解法二:利用Scosθ=S′.如右图,
解法二:利用Scosθ=S′.如右图,
平面PAD⊥平面ABCD

 CD⊥AD,BA⊥AD
CD⊥AD,BA⊥AD
BA⊥平面PAD

CD⊥平面PAD
△PAD是△PBC在平面PDA内的射影.设面PDA与面PCB所成的二面角为θ,则S△PDA=S△PCB·cosθ.Rt△PAB中,PA=4 =AD;Rt△PDC中,PD=2
=AD;Rt△PDC中,PD=2 .
.
∴△PAD为等腰三角形且S△PAD= PD·AH=15
PD·AH=15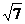 .
.
cosθ= =
=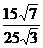 =
=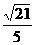 ,
,
θ=arccos=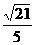 .
.
(七)平面与平面平行,平面与平面垂直
例7 如图,在△ABC中,AD⊥BC,E为AD上的三等分点,AE= ED,过E的直线MN∥BC,交AB、AC于M、N,将
ED,过E的直线MN∥BC,交AB、AC于M、N,将
△AMN折起到与平面MBCN成60°,求证:平面A′MN⊥平面A′BC.
 证明:∵AD⊥BC,BC∥MN
证明:∵AD⊥BC,BC∥MN
∴A′E和ED都垂直于MN,
∴∠A′ED是二面角A′MN-MN-MBCN的平面角, ∴∠A′ED=60°,A′E=AE= ED=ED·cos60°.
ED=ED·cos60°.
∴△A′ED是直角三角形,且A′E⊥A′D.
又∵A′E⊥MN,MN∥BC,
∴A′E⊥BC,而BC∩A′D=D.
∴A′E⊥平面A′BC,
∵A′E 面A′MN,
面A′MN,
∴平面A′MN⊥平面A′BC.
(六)异面直线所成的角、直线与平面所成的角
例6 把两个三角板ABC与ABD摆成如图所示的直二面角D-AB-C,求异面直线DC与AB所成的角.
 解:过C作CE∥AB,过D作DF⊥CE,垂足为F,连结AF,则∠DCF为异面直线DC与AB所成的角,设AC=BC=1,则AB=
解:过C作CE∥AB,过D作DF⊥CE,垂足为F,连结AF,则∠DCF为异面直线DC与AB所成的角,设AC=BC=1,则AB= ,AD=AB·tg30°=
,AD=AB·tg30°=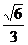 ,由三垂线定理的逆定理可证AF⊥CF,得等腰直角△ACF,则AF=
,由三垂线定理的逆定理可证AF⊥CF,得等腰直角△ACF,则AF=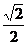 AC=
AC=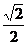 =CF.在Rt△DAF中,DF=
=CF.在Rt△DAF中,DF=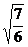 ,在Rt△DCF中,tg∠DCF=
,在Rt△DCF中,tg∠DCF=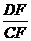 =
= .∴异面直线AB与DC所成的角为arctg
.∴异面直线AB与DC所成的角为arctg .
.
(五)三垂线定理及逆定理
例5 已知:如图,S为正方形ABCD所在平面外一点,SA⊥平面ABCD,过A作截面AEKH⊥SC.
 求证:AE⊥SB,AH⊥SD,AK⊥HE.
求证:AE⊥SB,AH⊥SD,AK⊥HE.
证明:
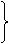 SA⊥平面ABCD
SA⊥平面ABCD

BC⊥AB
 BC⊥SB(三垂线定理)
BC⊥SB(三垂线定理)

BC⊥SA
 BC⊥平面SAB
BC⊥平面SAB BC⊥AE
BC⊥AE

又SC⊥平面AEKH SC⊥AE
SC⊥AE
AE⊥平面SBC AE⊥SB.
AE⊥SB.
同理可证AH⊥平面SDC,故AH⊥SD.又∵ABCD为正方形,∴Rt△SAD≌Rt△SAB.故SD=SB,SH=SE.
∴HE∥DB.SA⊥DB,则SA⊥HE,SK⊥平面AEKH,AK是SA在截面上的射影,故HE⊥AK(三垂线定理的逆定理).
(四)直线平面垂直的判定与性质定理
例4 已知如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若平面PDC与平面ABCD成45°角,求证:MN⊥平面PDC.
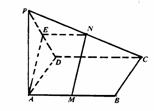 证明:取PD中点E,连接EN、EA.
证明:取PD中点E,连接EN、EA.
∵N是PC中点.
∴EN ∥  CD,CD=AB,
CD,CD=AB,
故ENMA是平行四边形,MN∥AE.
∵PA⊥面ABCD.
∴PA⊥AB.
又∵AB⊥AD,PA∩AD=A
∴AB⊥面PAD.
∵AE 面PAD,PD
面PAD,PD 面PAD,
面PAD,
∴AB⊥AE,AB⊥PD,MN⊥AB,从而MN⊥CD.
∵CD⊥AD,CD⊥PD.
∴∠PDA是二面角P-CD-A的平面角.
∴△PAD是等腰直角三角形,从而AE⊥PD,
故MN⊥PD,PD∩CD=D.
∴MN⊥平面PDC.
(三)直线与平面平行的判定与性质定理
例3 直角△ABC的一条边AB∩α=A,另一边BC不在平面α内,若∠ABC在α上的射影仍是直角,求证BC∥α.
证明:如图,过B、C分别作α的垂线,垂足分别为B′、C′,则∠AB′C′是∠ABC在α上的射影.
∴∠AB′C′=90°
 又∵BB′⊥α,AB′
又∵BB′⊥α,AB′ α,B′C′
α,B′C′ α,
α,
∴AB′⊥BB′,C′B′⊥BB′.
∵B′A∩BB′=B′,
∴C′B′⊥平面AB′B.
∵B′C′∩B′B=B′,
∴AB′⊥平面BB′C′C.
∵BC 面BB′C′C,
面BB′C′C,
∴BC⊥AB′.
∵∠ABC=90°,AB∩AB′=A,
∴BC⊥平面ABB′.
∴BC∥B′C′.
∴BC∥α.
(二)异面直线,两直线的位置关系,证明两直线异面、平行的一般方法
例2 求证:过两条平行线中的一条直线的平面,与另一条直线平行或经过另一条直线.
 已知:如图,a∥b,b
已知:如图,a∥b,b α.
α.
求证:a∥α或a α
α
证明:假设a∩α=A.
∵a∥b,A∈α,
∴A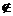 b
b
又∵a∩α=A,则a上至少有一点B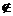 α.
α.
∴a、b是异面直线.
这和a∥b矛盾,故假设a∩α=A不成立.
即a∥α或a α.
α.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com