
2.圆
圆的定义
点集:{M||OM|=r},其中定点O为圆心,定长r为半径.
圆的方程
(1)标准方程
圆心在c(a,b),半径为r的圆方程是
(x-a)2+(y-b)2=r2
圆心在坐标原点,半径为r的圆方程是
x2+y2=r2
(2)一般方程
当D2+E2-4F>0时,一元二次方程
x2+y2+Dx+Ey+F=0
叫做圆的一般方程,圆心为(-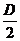 ,-
,- ,半径是
,半径是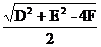 .配方,将方程x2+y2+Dx+Ey+F=0化为
.配方,将方程x2+y2+Dx+Ey+F=0化为
(x+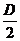 )2+(y+
)2+(y+ )2=
)2=
当D2+E2-4F=0时,方程表示一个点
(-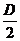 ,-
,- );
);
当D2+E2-4F<0时,方程不表示任何图形.
点与圆的位置关系 已知圆心C(a,b),半径为r,点M的坐标为(x0,y0),则
|MC|<r 点M在圆C内,
点M在圆C内,
|MC|=r 点M在圆C上,
点M在圆C上,
|MC|>r 点M在圆C内,
点M在圆C内,
其中|MC|= .
.
(3)直线和圆的位置关系
①直线和圆有相交、相切、相离三种位置关系
直线与圆相交 有两个公共点
有两个公共点
直线与圆相切 有一个公共点
有一个公共点
直线与圆相离 没有公共点
没有公共点
②直线和圆的位置关系的判定
(i)判别式法
(ii)利用圆心C(a,b)到直线Ax+By+C=0的距离d= 与半径r的大小关系来判定.
与半径r的大小关系来判定.
1.方程的曲线
在平面直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹 )上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点.那么这个方程叫做曲线的方程;这条曲线叫 做方程的曲线.
点与曲线的关系 若曲线C的方程是f(x,y)=0,则点P0(x0,y0)在曲线C上 f(x0,y 0)=0;
f(x0,y 0)=0;
点P0(x0,y0)不在曲线C上 f(x0,y0)≠0
f(x0,y0)≠0
两条曲线的交点 若曲线C1,C2的方程分别为f1(x,y)=0,f2(x,y)=0,则
 f1(x0,y0)=0
f1(x0,y0)=0
点P0(x0,y0)是C1,C2的交点
f2(x0,y0) =0
方程组有n个不同的实数解,两条曲线就有n个不同的交点;方程组没有实数解,曲线就没有 交点.
4.了解用坐标法研究几何问题的思想,初步掌握利用方程研究曲线性质的方法.
3.理解坐标变换的意义,掌握利用坐标轴平移化简圆锥曲线方程的方法.
2.掌握圆锥曲线的标准方程及其几何性质,并根据并给的条件画圆锥曲线,了解圆锥曲线的 一些实际应用.
1.掌握直角坐标系中的曲线与方程的关系和轨迹的概念,能够根据所给条件,选择适当的直 角坐标系求曲线的方程,并画出方程所表示的曲线.
(三)解答题
16.已知平面α和不在这个平面内的直线a都垂直于平面β,求证a∥α.
17.如图,正方形ABCD,E、F分别是AB、CD的中点,G为BF的中点,现将正方形沿EF折成120°的二面角.求①异面直线EF和AG所成的角;②AG和平面EBCF所形成的角.
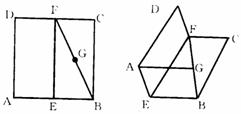
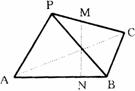
第17题图 第18题图
18.如图,已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.①求证MN⊥AB;②∠APB=90°,BC=2,AB=4时,求MN的长.
19. 如图,已知二面角α-PQ-β为60°,点A和B分别在平面α和平面β内,点C在棱PQ上,且∠ACP=∠BCP=30°AC=BC①求证AB⊥PQ;②求直线PQ
如图,已知二面角α-PQ-β为60°,点A和B分别在平面α和平面β内,点C在棱PQ上,且∠ACP=∠BCP=30°AC=BC①求证AB⊥PQ;②求直线PQ
在面ABC所成角的大小.

20.如图,已知矩形ABCD中,AB=1,BC=a(a>0,PA⊥平面AC,且PA=1.①问BC边上是否存在点Q,使得PQ⊥QD,并说明理由;②若BC边上有且只有一个点Q使得PQ⊥QD,求这时二面角Q-PD-A的大小.
(二)填空题
11.两条异面直线所成的角为θ,则cosθ的取值范围是_________.
12.棱长为1的正方体,PA、PB、PC是共一个顶点P的三条棱,那么点P到平面ABC的距离是_________.
13.从三棱锥六条棱的中点中,任选四个作为四边形的顶点.其中为平行四边形的个数有__________个.
14.二面角的一个面内有一条直线与另一个面成30°,这直线与棱成45°角,则此二面角度数_________.
15.正四棱锥S-ABCD的高为2,底面边长为 ,P、Q两点分别在线段BD和SC上,则P、Q两点的最短距离为_______.
,P、Q两点分别在线段BD和SC上,则P、Q两点的最短距离为_______.
(一)选择题
1.下列命题中,假命题是( )
A.若a,b是异面直线,则一定存在平面α过a且与b平行
B.若a,b是异面直线,则一定存在平面α与a且与b垂直
C.若a,b是异面直线,则一定存在平面α与a,b所成的角相等
D.若a,b是异面直线,则一定存在平面α与a,b的距离相等
2.下列命题中,真命题是( )
A.若直线m、n都平行于平面α则m∥n
B.设α-l-β是直二面角,若直线m⊥l,则m⊥β
C.若m、n在平面α内的射影依次是一个点和一条直线,且m⊥n,则n在α内或n与α平行
D.若直线m、n是异面直线,若m与平面α平行,则n与α平行,则n与α相交
3.如果直线l、m与平面α、β、γ满足:l=β∩γ,l∥α,m α和m⊥γ,那么必有( )
α和m⊥γ,那么必有( )
A.α⊥γ且l⊥m B.α⊥γ且m∥β C.m∥β且l⊥m D.α∥β且α⊥γ
4.设α、β是两个不重合的平面,m和l是两条不重合的直线,则α∥β的一个充分条件是( )
A.l α,m
α,m α且l∥β,m∥β B.l
α且l∥β,m∥β B.l α,m
α,m β且l∥m
β且l∥m
C.l⊥α,m⊥β,且l∥m D.l∥α,m∥β且l∥m
5.已知直二面角α-l-β,直线m a,直线n
a,直线n β,且m、n均不与直线l垂直,则( )
β,且m、n均不与直线l垂直,则( )
A.m和n不可能垂直,但可能平行 B.m与n可能垂直,但不能平行
C.m和n可能垂直,也可能平行 D.m与n不能垂直,也不能平行
6.二面角α-EF-β是直二面角,C∈EF,AC α,BC
α,BC β,如果∠ACF=30°,∠ACB=60°,∠BCF=θ,那么cosθ的值等于,则( )
β,如果∠ACF=30°,∠ACB=60°,∠BCF=θ,那么cosθ的值等于,则( )
A. B.
B.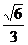 C.
C.
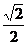 D.
D.

7.如图,有共同底边的等边△ABC和等边三角形BCD所在平面互相垂直,则异面直线AB和CD所成角的余弦值为( )
 A.
A. B.
B.  C.
C. D.
D.
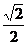
8.正方体ABCD-A1B1C1D1中截面AB1C和截面A1B1C所成的二面角的大小为( )
 A.45° B.60°
C.arccos
A.45° B.60°
C.arccos D.arccos
D.arccos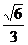
9.如图,BCDE是一个正方形,AB⊥平面CE,侧图中相互垂直的平面有( )
A.3组 B.6组 C.7组 D.8组
10.菱形ABCD的边长为a,∠A=60°,E、F、G、H分别在AB,BC,CD,DA上,且BE=BF=DG=DH= ,沿EH与FG把
,沿EH与FG把
菱形的两个锐角对折起来,使A、C两点重合,这时A点到平面E-FGH的距离为( )
A.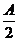 B.
B. C.
C.
 D.(
D.( -1)a
-1)a
(二)空间直线和平面
例15 已知直线l垂直于平面α,直线m 平面β,有下面四个命题:
平面β,有下面四个命题:
(1)α∥β l⊥m
l⊥m
(2)α⊥β l∥m
l∥m
(3)l∥m α⊥β
α⊥β
(4)l⊥m α∥β
α∥β
其中正确的两个命题是( )
A.(1)与(2) B.(3)与(4) C.(2)与(4) D.(1)与(3)
解:命题(1)正确,证明如下:
∵l⊥α,若α∥β,则l⊥β,
又m β,
β,
∴l⊥m
命题(2)不正确.
已知l⊥α,β⊥α,此时有可能l β,又因m
β,又因m β,从而l与m共面β,l和m可能平行也可能相交.
β,从而l与m共面β,l和m可能平行也可能相交.
命题(3)正确,证明如下:
∵l⊥α,l∥m,
∴m⊥α,
又m β,
β,
∴α⊥β.
命题(4)不正确,
设α∩β=m,∵l⊥α,m α,∴l⊥m,故由l⊥α,m?β,l⊥m
α,∴l⊥m,故由l⊥α,m?β,l⊥m α∥β.
α∥β.
(1)、(3)正确;(2)、(4)不正确.
应选D.
例16 如图(1),ABCD是正方形,E是AB中点,如将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,
记A与B重合后的点为P,则面PCD与面ECD所成的二面角为_________度.
 解:在图(2)上作PH⊥CD于H,设正方形ABCD的边长1.
解:在图(2)上作PH⊥CD于H,设正方形ABCD的边长1.
易知PD=l,PC=l,∴H为DC中点.
又ED=EC.
∴EH⊥DC于H.
设∠PHE=θ,则θ为面PCD与面ECD所成二面角的大小.
在△PDC中,由PD=PC=DC=l,得PH= ,
,
在△EDC中,由EH=
=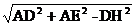 =l,
=l,
又P是A、B重合的点,故PE=AE= .
.
用余弦定理于△PHE,有
cosθ=cos∠PHE=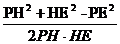 =
= =
= ,
,
由于θ∈(0,180°),得θ=30°.
应填30°.

 例17 已知:如图,平面α∩平面β=直线a,α、β同时垂直于平面r,又同时平行于直线b.
例17 已知:如图,平面α∩平面β=直线a,α、β同时垂直于平面r,又同时平行于直线b.
求证:(1)a⊥γ,(2)b⊥γ.
证明:(1)设α∩γ=m,β∩γ=n.
在直线a上任选不在平面γ上的点A,作AO⊥m于O,AO′⊥n于O′.
∵AO α,α⊥γ且α∩γ=m,AO⊥m,
α,α⊥γ且α∩γ=m,AO⊥m,
∴AO⊥γ(两面垂直,则在其中一个平面上且垂直于交线的直线必垂直于另一个面).同理AO′⊥γ.
但平面γ外的点A在平面γ的射影唯一.
∴O和O′重合于m,n的交点.
即直线a⊥平面γ.
(2)∵b∥平面α,
∴存在b′ α,b′≠a;满足b∥b′.
α,b′≠a;满足b∥b′.
又b∥β,从而b′∥β.
因为平面α过b′且交平面β于a,
∴b′∥a,从而b∥a.
由a⊥γ,得b⊥γ.
例18 如果直线l,m与平面α、β、γ满足:l=β∩r,l∥α
,m α,和m⊥γ,那么必有( )
α,和m⊥γ,那么必有( )
A.α⊥γ且l⊥m
B.α⊥γ且m∥β
C.m∥β且l⊥m
D.α∥β且α⊥γ
解:∵m α,m⊥γ,
α,m⊥γ,
∴γ⊥α,
∵l γ,m⊥γ,
γ,m⊥γ,
∴m⊥l.
即在题设的条件下必有γ⊥α且l⊥m.
应选A.
例19 如图1-37,在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
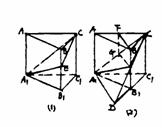 (1)求证:BE=EB1;
(1)求证:BE=EB1;
(2)若AA1=A1B1,求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
注意:在下面横线上填写适当内容,使之成为(1)的完成证明,并解答(2).
证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
(Ⅰ)∵_____________________
∴EG⊥侧面AC1,取AC的中点F,连结BF、FG,由AB=BC得BF⊥FC.
(Ⅱ)∵_____________________
∴BF⊥侧面AC1,得BF∥EG,BF、EG确定一个平面,交侧面AC1于FC.
(Ⅲ)∵_____________________
∴BF∥EG,四边形BEGF是平行四边形,BE=FG.
(Ⅳ)∵_____________________
∴FG∥AA1,ΔAA1C∽ΔFGC,
(Ⅴ)∵_____________________
∴FG= AA1=
AA1= BB1,即BE=
BB1,即BE= BB1,故BE=EB1.
BB1,故BE=EB1.
解:(1) (Ⅰ)∵面A1EC⊥侧面AC1,
(Ⅱ)∵而面ABC⊥侧面AC1,
(Ⅲ)∵BE∥侧面AC1,
(Ⅳ)∵BE∥AA1,
(Ⅴ)∵AF=FC.
(2)分别延长CE、C1B1交于点D,连结A1D.
∵EB1∥CC1,EB1= BB1=
BB1= CC1,
CC1,
∴DB1= DC1=B1C1=A1B1,
DC1=B1C1=A1B1,
∵∠B1A1C1=∠B1C1A1=60°
∠DA1B1=∠A1DB1= (180°-∠DB1A1)=30°
(180°-∠DB1A1)=30°
即DA1⊥A1C1
∵CC1⊥面A1C1B1,即A1C1在平面A1C1D上的射影,根据三垂线定理得DA1⊥A1C,
∴∠CA1C是所求二面角的平面角.
∵CC1=AA1=A1B1=A1C1,∠A1C1C=90°,
∴∠CA?1C?1=45°,即所求二面角为45°.
例20 在空间中,下列命题成立的是( )
A.过平面α外的两点,必有且只有一个平面与平面α垂直
B.若直线l上有两点到平面α的距离相等,则直线l必平行于平面α
C.若直线l与平面α内的无数多条直线垂直,则直线l必垂直于平面α
D.互相平行的两条直线在一个平面内的射影仍然是互
相平行的两条直线
E.若点P到三角形的三条边的距离相等,则点P在该
三角形所在平面内的射影必然是该三角形的内心
解:A不正确.若平面α外的两点A、B使直线AB⊥α,则过A、B两点且与α垂直的平面有无数多个.
B不正确.设l和α交于点O,在l上取OA=OB,则A、B到平面α等距但直线AB不平行于平面α.
C不正确.设l斜交α于O,在α内过O点作m⊥l,则α内与m平行的无数多条直线都平行于l,但l与α不垂直.
D不正确.若互相平行的两直线a,b所确定的平面β⊥α,则a,b在α内的射影是一条直线.
E正确.由三垂线定理易证明它的正确性.
例21 已知二面角α-AB-β的平面角是锐角θ,α内一点C到β的距离为3,点C到棱的距离为4,那么tgθ的值等于( )
A. B.
B.
 C.
C. D.
D. .
.
解:如图,CO⊥β于O,CD⊥AB于D,则CO=3,CD=4,∠CDO=θ,∠COD=90°.
 ∴tgθ=
∴tgθ= =
=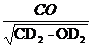
= =
= .
.
应选C.
例22 下列命题中,错误的是( )
A.若一直线垂直于一平面,则此直线必垂直于这平面上所有的直线
B.若一个平面通过另一个平面的一条垂线,则这两个平面互相垂直
C.若一条直线垂直于一个平面的一条垂线,则此直线平行于这个平面
D.若平面内的一条直线和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直
解:B为两面垂直的一个判定定理.
A为线面垂直的性质定理.
C错误:设l⊥平面α,m∥l,若m?α,则m∥α.
应选C.
例23 下列四个命题中的真命题是( )
A.若直线l平面α内两条平行直线垂直,则l⊥α
B.若平面α内两条直线与平面β内两条直线分别平行,则α∥β
C.若平面α与直二角β-MN-r,棱MN交于点A,与二面角的面β,而r分别交于AB、AC,则∠BAC≤90°
D.以上三个命题都是假命题.
解:命题A不真
命题B不真;若这四条直线都平行,则有可能α∥β
 命题C不真:
命题C不真:
如图
BC2 =BB′2+BC′2
=BB′2+CC′2+B′C2
=BB′2+CC′2+(B′A+C′A)2
>BB′2+CC′2+B′A′2+C′A2
=(BB′2+B′A2)+(CC′2+C′A2)
=BA2+CA2
∴∠BAC>90°
应选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com