
(七)坐标轴的平移,利用坐标的平移化简圆锥曲线方程
说明 坐标轴的平移变换是化简曲线方程的一种重要方法.掌握平移坐标轴的 关键在于正确理解新旧坐标系之间的关系.同一个点在不同的坐标系中有不同的坐标,同一 条曲线在不同的坐标中有不同的方程.
例7 方程x2+4y2+6x-8y+1=0的对称中心是( )
A.(-3,-1) B.(-3,1) C.(3,-1) D.(3,1)
解: 将原方程配方后化为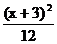 +
+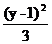 =1,∴ 对称中心是(-3,1).故选B.
=1,∴ 对称中心是(-3,1).故选B.
例8 求椭圆9x2+4y2-36x+8y+4=0的焦点坐标、长轴与短轴的长、离心率 及准线方程.
解: 将原方程配方后化成
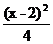 +
+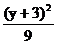 =1.
=1.
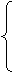 x′=x-2
x′=x-2
令
得到新方程为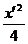 +
+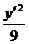 =1.
=1.
y′=y+3
∴a=3,b=2,c=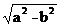 =
=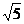 .
.
即长轴长2a=6,短轴长2b=4,离心率e= =
=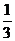
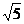 .在新坐标系中,焦点为(0,
.在新坐标系中,焦点为(0,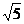 ),(0,-
),(0,-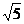 ),
),
准线为y′=±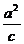 =±
=±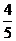
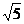
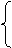 x=x′+2
x=x′+2
由平移公式 ,得在原坐标系中
y=y′-3
焦点为:(2,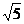 -3)、(2,-
-3)、(2,-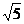 -3),
-3),
准线为:y=±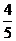
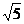 -3.
-3.
(六)抛物线及其标准方程,焦点、准线、抛物线的几何性质:范围、对称性、顶点、离心率,抛物线的画法
说明 这部分内容要注意与初中讲的抛物线y=ax2+bx+c(c≠0)的关系,以及抛物线与双曲线一支的区别,y=ax2+bx+c的对称轴平行于y轴(或就是y轴),双曲线有渐近线,抛物线无渐近线.
例6 圆心在抛物线y2=2x上,且与x轴相切的一个圆的方程是( )
A.x2+y2-x-2y- =0 B.x2+y2+x-2y+1=0 C.x2+y2-x-2y+1=0 D.x2+y2-x-2y+
=0 B.x2+y2+x-2y+1=0 C.x2+y2-x-2y+1=0 D.x2+y2-x-2y+ =0
=0
解: 经过配方将四个选项中圆的一般方程化为标准方程.
①(x-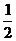 )2+(y-1)2=
)2+(y-1)2=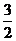 ②(x+
②(x+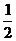 )2+(y-1)2=
)2+(y-1)2=
③(x-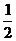 )2+(y-1)2=
)2+(y-1)2= ④(x-
④(x-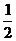 )2+(y-1)2=1
)2+(y-1)2=1
由已知条件,②的圆心不在抛物线y2=2x上.而圆要与x轴相切,则圆心的纵坐标的绝对值 要等于半径.故只有④适合.选D.
(五)双曲线及其标准方程,焦点、焦距,双曲线的几何性质:范围、对称 性、顶点、实轴、虚轴、渐近线、离心率、准线,双曲线的画法,等边双曲线
说明 根据已知条件会求双曲线的标准方程,以及双曲线的有关元素.这里 与椭圆不同的是实轴、虚轴和渐近线.
例5 已知双曲线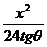 -
-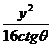 =1(
=1( <θ<π)过点
<θ<π)过点
A(4 ,4).
,4).
(1)求实轴、虚轴的长;
(2)求离心率;
(3)求顶点坐标;
(4)求点A的焦半径.
解: 因为双曲线过点A(4 ,4),所以
,4),所以
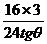 -
-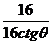 =1,tg2+tgθ-2=0 ,tgθ=-2,(tgθ=1舍去,因为
=1,tg2+tgθ-2=0 ,tgθ=-2,(tgθ=1舍去,因为 <θ<π=
<θ<π=
∴双曲线方程为-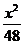 +
+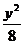 =1.
=1.
从而a=2 ,b=4
,b=4 ,c=2
,c=2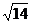 .
.
(1)实轴长2a=4 ,虚轴长2b=8
,虚轴长2b=8 .
.
(2)离心率e= =
=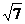 .
.
(3)顶点为(0,2 ),(0,-2
),(0,-2 ).
).
(4)焦点F1(0,-2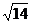 ),F2(0,2
),F2(0,2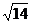 ).
).
|AF1|=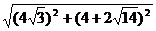
=2 (
(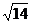 +1),
+1),
|AF2|=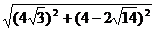
=2 (
(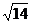 -1).
-1).
(四)椭圆及其标准方程,焦点、焦距,椭圆的几何性质:范围、对称性、顶 点、长袖、短轴、离心率、准线,椭圆的画法
说明 天体的运行轨道基本都是椭圆,所以掌握椭圆的基本概念是很有必要 的.考试说明中明确要求,要会求椭圆的标准方程和椭圆的有关元素.
例4 P是椭圆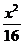 +
+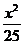 =1上 的点,F1、F2为其焦点,若∠F1PF2=90°.求ΔPF1F2的面积.
=1上 的点,F1、F2为其焦点,若∠F1PF2=90°.求ΔPF1F2的面积.
解:∵S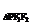 =
=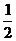 |PF1|·|PF2|,而|PF2 |+|PF2|=10,
|PF1|·|PF2|,而|PF2 |+|PF2|=10,
|PF1|2+|PF2|2=|F1F2|2=36,联合求解得:
PF1·PF2= =32,
=32,
∴S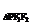 =16.
=16.
(三)圆的标准方程和一般方程
说明 求圆的方程主要是求出其圆心与半径.还要掌握一般方程与标准方程 的互化,以及圆与其他曲线之间的关系,特别是圆与直线之间的关系.
例3 圆A:(x+1)2+(y+1)2=1,
圆B:(x-1)2+(y-1)2=4,则有两圆的公切线有( )
A.1条 B.2条 C.3条 D.4条
解: 要判断两圆公切线的条数,只需要判断出此两圆的位置关系,而不必求出其切线方程 . ∵A圆圆心是C1(-1,-1),B圆圆心是C2(1,1),∴|C1C2|=2 ,r1=1,r2=2.
,r1=1,r2=2.
r1+r2>|C1C2|即圆A与圆B相离,则此两圆有4条公切线.故选D.
(二)充要条件
说明 充分条件、必要条件、充要条件是高考考查的重要内容.要掌握好这 几种条件,关键在于要对命题之间的关系很清楚.
例2 设甲、乙、丙是三个命题,如果甲是乙的必要条件;丙是乙的充分条件,但不是乙的必要条件,那么( )
A.丙是甲的充分条件,但不是甲的必要条件 B.丙是甲的必要条件,但不是甲的充分条件
C.丙是甲的充要条件, D.丙不是甲的充分条件,也不是甲的必要条件
解: 由已知乙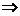 甲,丙
甲,丙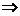 乙,所以丙
乙,所以丙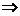 甲,即丙 是甲的充分条件,故选A.
甲,即丙 是甲的充分条件,故选A.
(一)曲线和方程,由已知条件列出曲线的方程,曲线的交点
说明 在求曲线方程之前必须建立坐标系,然后根据条件列出等式进行化简 .特别是在求出方程后要考虑化简的过程是否是同解变形,是否满足已知条件,只有这样求 出的曲线方程才能准确无误.另外,要求会判断 曲线间有无交点,会求曲线的交点坐标.
例1 如果实数x、y满足等式(x-2)2+y2=3,求y/x的最大值.
解: 此题有多种解法,但用待定参数,转化为求曲线的交点问题可使解题过程更为简捷.
设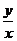 =k,则y=kx.要使k的值最大,只须直线y=kx在第一象限与圆相切
,而圆心(2,0)到直线y=kx的距离为
=k,则y=kx.要使k的值最大,只须直线y=kx在第一象限与圆相切
,而圆心(2,0)到直线y=kx的距离为 .
.
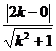 =
= ,解得k=
,解得k= (-
(- 舍去).
舍去).
5.坐标变换
坐标变换 在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做 坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点 的坐标与曲线的方程.
坐标轴的平移 坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫 做坐标轴的平移,简称移轴.
坐标轴的平移公式 设平面内任意一点M,它在原坐标系xOy中的坐标是9x,y),在新坐标系x ′O′y′中的坐标是(x′,y′).设新坐标系的原点O′在原坐标系xOy中的坐标是(h,k),则
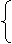
 x=x′+h
x′=x-h
x=x′+h
x′=x-h
(1) 或(2)
y=y′+k y′=y-k
公式(1)或(2)叫做平移(或移轴)公式.
中心或顶点在(h,k)的圆锥曲线方程
中心或顶点在(h,k)的圆锥曲线方程见下表.
|
方 程 |
焦 点 |
焦 线 |
对称轴 |
|
|
椭圆 |
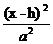 + + =1 =1 |
(±c+h,k) |
x=±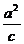 +h +h |
x=h y=k |
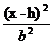 + + =1 =1 |
(h,±c+k) |
y=±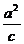 +k +k |
x=h y=k |
|
|
双曲线 |
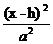 - - =1 =1 |
(±c+h,k) |
=±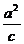 +k +k |
x=h y=k |
 - -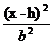 =1 =1 |
(h,±c+h) |
y=±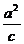 +k +k |
x=h y=k |
|
|
抛物线 |
(y-k)2=2p(x-h) |
(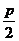 +h,k) +h,k) |
x=-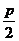 +h +h |
y=k |
|
(y-k)2=-2p(x-h) |
(-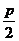 +h,k) +h,k) |
x=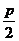 +h +h |
y=k |
|
|
(x-h)2=2p(y-k) |
(h, 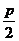 +k) +k) |
y=-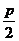 +k +k |
x=h |
|
|
(x-h)2=-2p(y-k) |
(h,- 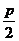 +k) +k) |
y=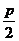 +k +k |
x=h |
4.圆锥曲线的统一定义
平面内的动点P(x,y)到一个定点F(c,0)的距离与到不通过这个定点的一条定直线l的距离之 比是一个常数e(e>0),则动点的轨迹叫做圆锥曲线.
其中定点F(c,0)称为焦点,定直线l称为准线,正常数e称为离心率.
当0<e<1时,轨迹为椭圆
当e=1时,轨迹为抛物线
当e>1时,轨迹为双曲线
3.椭圆、双曲线和抛物线
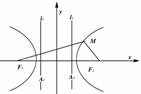
椭圆、双曲线和抛物线的基本知识见下表.
 |
椭 圆 |
双曲线 |
抛物线 |
|||
|
轨迹条件 |
点集:({M||MF1+|MF2|=2a,|F 1F2|<2a= |
点集:{M||MF1|-|MF2|. =±2a,|F2F2|>2a}. |
点集{M| |MF|=点M到直线l的距离}. |
|||
|
圆 形 |
|
 |
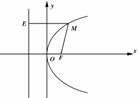 |
|||
|
标准方程 |
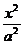 + +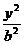 =1(a>b>0) =1(a>b>0) |
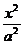 - -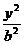 =1(a>0,b>0) =1(a>0,b>0) |
y2=2px(p>0) |
|||
|
顶 点 |
A1(-a,0),A2(a,0); B1(0,-b),B2(0,b) |
A1(0,-a),A2(0,a) |
O(0,0) |
|||
|
轴 |
对称轴x=0,y=0 长轴长:2a 短轴长:2b |
对称轴x=0,y=0 实轴长:2a 虚轴长:2b |
对称轴y= |
|||
|
焦 点 |
F1(-c,0),F2(c,0) 焦点在长轴上 |
F1(-c,0),F2(c,0) 焦点在实轴上 |
F(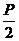 ,0) ,0)焦点对称轴上 |
|||
|
焦 距 |
|F1F2|=2c, c= 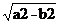 |
|F1F2|=2c, c= 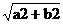 |
|
|||
|
准 线 |
x=±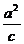 准线垂直于长轴,且在椭圆外. |
x=±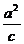 准线垂直于实轴,且在两顶点的内侧. |
x=-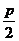 准线与焦点位于顶点两侧,且到顶点的距离相等. |
|||
|
离心率 |
e= ,0<e<1 ,0<e<1 |
e= ,e>1 ,e>1 |
e=1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com