
4.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)若点P为l上的动点,求∠F1PF2最大值.
本题主要考查椭圆的几何性质、椭圆方程、两条直线的夹角等基础知识,考查解析几何的基本思想方法和综合解题能力.满分14分.
解:(Ⅰ)设椭圆方程为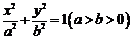 ,半焦距为
,半焦距为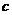 ,则
,则

(Ⅱ)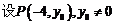

3.(本小题满分14分)
已知不等式 为大于2的整数,
为大于2的整数, 表示不超过
表示不超过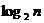 的最大整数. 设数列
的最大整数. 设数列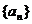 的各项为正,且满足
的各项为正,且满足
(Ⅰ)证明
(Ⅱ)猜测数列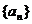 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当 时,对任意b>0,都有
时,对任意b>0,都有
本小题主要考查数列、极限及不等式的综合应用以及归纳递推的思想.
(Ⅰ)证法1:∵当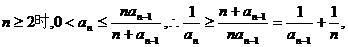
即
于是有 
所有不等式两边相加可得 
由已知不等式知,当n≥3时有,
∵
证法2:设 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式

(i)当n=3时, 由 
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即
则

即当n=k+1时,不等式也成立.
由(i)、(ii)知,
又由已知不等式得 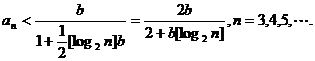
(Ⅱ)有极限,且
(Ⅲ)∵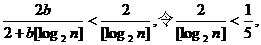
则有
故取N=1024,可使当n>N时,都有
2.(本小题满分12分)
设A、B是椭圆 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定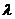 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的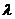 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(此题不要求在答题卡上画图)
本小题主要考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力.
(Ⅰ)解法1:依题意,可设直线AB的方程为 ,整理得
,整理得  ①
①
设 是方程①的两个不同的根,
是方程①的两个不同的根,
∴ ②
②
且 由N(1,3)是线段AB的中点,得
由N(1,3)是线段AB的中点,得
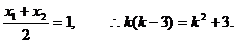
解得k=-1,代入②得, 的取值范围是(12,+∞).
的取值范围是(12,+∞).
于是,直线AB的方程为
解法2:设 则有
则有

依题意,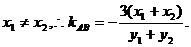
∵N(1,3)是AB的中点, ∴
又由N(1,3)在椭圆内,∴
∴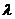 的取值范围是(12,+∞).
的取值范围是(12,+∞).
直线AB的方程为y-3=-(x-1),即x+y-4=0.
(Ⅱ)解法1:∵CD垂直平分AB,∴直线CD的方程为y-3=x-1,即x-y+2=0,
代入椭圆方程,整理得 
又设 CD的中点为
CD的中点为 是方程③的两根,
是方程③的两根,
∴
于是由弦长公式可得  ④
④
将直线AB的方程x+y-4=0,代入椭圆方程得 ⑤
⑤
同理可得 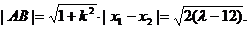 ⑥
⑥
∵当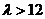 时,
时,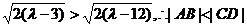
假设存在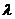 >12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
点M到直线AB的距离为  ⑦
⑦
于是,由④、⑥、⑦式和勾股定理可得
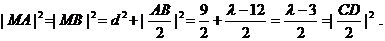
故当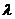 >12时,A、B、C、D四点匀在以M为圆心,
>12时,A、B、C、D四点匀在以M为圆心, 为半径的圆上.
为半径的圆上.
(注:上述解法中最后一步可按如下解法获得:)
A、B、C、D共圆 △ACD为直角三角形,A为直角
△ACD为直角三角形,A为直角 |AN|2=|CN|·|DN|,
|AN|2=|CN|·|DN|,
即  ⑧
⑧
由⑥式知,⑧式左边
由④和⑦知,⑧式右边
∴⑧式成立,即A、B、C、D四点共圆.
解法2:由(Ⅱ)解法1及λ>12,
∵CD垂直平分AB, ∴直线CD方程为 ,代入椭圆方程,整理得
,代入椭圆方程,整理得
 ③
③
将直线AB的方程x+y-4=0,代入椭圆方程,整理得
 ⑤
⑤
解③和⑤式可得

不妨设
∴

计算可得 ,∴A在以CD为直径的圆上.
,∴A在以CD为直径的圆上.
又B为A关于CD的对称点,∴A、B、C、D四点共圆.
(注:也可用勾股定理证明AC⊥AD)
1.(本小题满分14分)
如图,设抛物线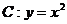 的焦点为F,动点P在直线
的焦点为F,动点P在直线 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
解:(1)设切点A、B坐标分别为 ,
,
∴切线AP的方程为:
切线BP的方程为: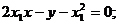
解得P点的坐标为:
所以△APB的重心G的坐标为 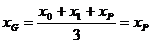 ,
,

所以 ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为:
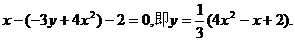
(2)方法1:因为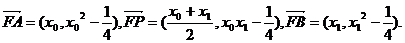
由于P点在抛物线外,则
∴
同理有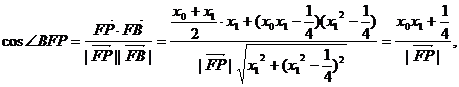
∴∠AFP=∠PFB.
方法2:①当 所以P点坐标为
所以P点坐标为 ,则P点到直线AF的距离为:
,则P点到直线AF的距离为:
即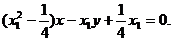
所以P点到直线BF的距离为: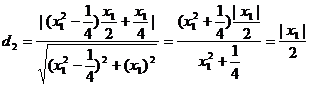
所以d1=d2,即得∠AFP=∠PFB.
②当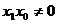 时,直线AF的方程:
时,直线AF的方程:
直线BF的方程:
所以P点到直线AF的距离为:
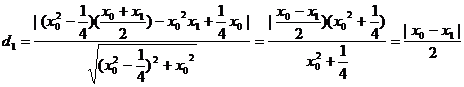 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离 ,因此由d1=d2,可得到∠AFP=∠PFB.
,因此由d1=d2,可得到∠AFP=∠PFB.
20. (上海市2009届高三上期期末浦东区)如图(a)所示电路中,电源电动势E=12V,内阻r=2Ω,R1=4Ω,R2=6Ω,R3=3Ω。
(上海市2009届高三上期期末浦东区)如图(a)所示电路中,电源电动势E=12V,内阻r=2Ω,R1=4Ω,R2=6Ω,R3=3Ω。
(1)若在C、D间连一个理想电压表,其读数是多少?
(2)若在C、D间连一个理想电流表,其读数是多少?
(3)图(a)中虚线框内的电路可等效为一个电源,即图(a)可等效为图(b),其等效电动势E′等于CD间未接入用电器时CD间的电压;若用导线直接将CD两点连接起来,通过该导线的电流等于等效电源的短路电流。则等效电源的内电阻r′是多少?
(4)若在C、D间连一个“6V,3W”的小灯泡,则小灯泡的实际功率是多少?
解析:.
(1)若在C、D间连一个理想电压表,根据闭合电路欧姆定律,有

理想电压表读数为
UV=I1R2=6V
(2)若在C、D间连一个理想电流表,这时电阻R2与R3并联,并联电阻大小


根据闭合电路欧姆定律,有
 理想电流表读数为
理想电流表读数为

(3)依题意,该等效电源的电动势 ,
,
短路电流 ,所以其等效内阻
,所以其等效内阻
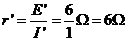
(4)小灯泡的电阻

将小灯泡连在C、D之间,相当于接在等效电源E′两端,则流过小灯泡的电流大小为

小灯泡的实际功率为

19.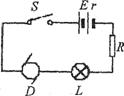 (2009年江苏天一中学高三月考)如图所示,已知电源电动势E=20V,内阻r=lΩ,当接入固定电阻R=4Ω时,电路中标有“3V,
6W”的灯泡L和内阻RD=0.5Ω的小型直流电动机D都恰能正常工作.试求:
(2009年江苏天一中学高三月考)如图所示,已知电源电动势E=20V,内阻r=lΩ,当接入固定电阻R=4Ω时,电路中标有“3V,
6W”的灯泡L和内阻RD=0.5Ω的小型直流电动机D都恰能正常工作.试求:
(1)电路中的电流大小;
(2)电动机的额定电压;
(3)电动机的输出功率.
答案:⑴灯泡L正常发光,电路中的电流为
⑵由闭合电路欧姆定律可求得,电动机的额定电压为
UD=E-I(r+R)-UL=20-2×(1+4)-3=7V
⑶电动机的总功率为P总=IUD=2×7=14W 电动机的热功率为P热=I2RD=22×0.5=2W
所以电动机的输出功率为P出=P总-P热=14-2=12W
18.(2009年北京西城区期末).在如图甲所示的电路中,螺线管匝数n = 1500匝,横截面积S = 20cm2。螺线管导线电阻r = 1.0Ω,R1 = 4.0Ω,R2 = 5.0Ω,C=30μF。在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化。求:
(1)求螺线管中产生的感应电动势;
(2)闭合S,电路中的电流稳定后,求电阻R1的电功率;
(3)S断开后,求流经R2的电量。
解:(1)根据法拉第电磁感应定律
求出 E = 1.2(V)
(2)根据全电路欧姆定律

根据 
求出 P = 5.76×10-2(W)
(3)S断开后,流经R2的电量即为S闭合时C板上所带的电量Q
电容器两端的电压 U = IR2=0.6(V)
流经R2的电量 Q = CU = 1.8×10-5(C)
16. (2009年崇明县高三期末)由门电路构成的一简单控制电路如图,其中R’为光敏电阻,光照时电阻很小,R为变阻器,L为小灯泡。其工作情况是:当光敏电阻受到光照时,小灯L不亮,不受光照时,小灯L亮。该逻辑电路是________门电路,该控制电路可以用在__________________________控制系统中(举一个例子)。
(2009年崇明县高三期末)由门电路构成的一简单控制电路如图,其中R’为光敏电阻,光照时电阻很小,R为变阻器,L为小灯泡。其工作情况是:当光敏电阻受到光照时,小灯L不亮,不受光照时,小灯L亮。该逻辑电路是________门电路,该控制电路可以用在__________________________控制系统中(举一个例子)。
答案: 非; 城市路灯等
17(2009年上海虹口区期末)居民小区里的楼道灯,采用门电路控制,电路如图所示。白天的时候,即使拍手发出声音,楼道灯也不亮;但是到了晚上,拍手发出声音后,灯就亮了,并采用延时电路,使之亮一段时间后就熄灭。电路中用声控开关,即听到声音后,开关闭合,则应该使用__________门电路控制电灯,其中R2是光敏电阻,受光照后电阻减小,R1为定值电阻,S是声控开关,黑夜时R1和R2的大小关系是R1______R2(选填“< <”、“=”或“> >”)。
答案: 与, , <<
15.(2009年北京丰台区高三上学期期末).如图所示,电源电动势为E=10V,内阻r=1Ω,R1=3Ω,R2=6Ω,C=30μF。开关S断开时,电容器的电荷量为 C。闭合开关S,稳定后通过R1的电流为 A。
答案 3×10-4; 1:
14. (北京崇文区2009届高三期末试题)用如图所示的实验电路研究微型电动机的性能。当调节滑动变阻器R,让电动机停止转动时,电流表和电压表的示数分别为0.50 A和2.0 V;重新调节R,使电动机恢复正常运转时,电流表和电压表的示数分别为2.0 A和24 V。则这台电动机(不计温度对电阻的影响) ( )
(北京崇文区2009届高三期末试题)用如图所示的实验电路研究微型电动机的性能。当调节滑动变阻器R,让电动机停止转动时,电流表和电压表的示数分别为0.50 A和2.0 V;重新调节R,使电动机恢复正常运转时,电流表和电压表的示数分别为2.0 A和24 V。则这台电动机(不计温度对电阻的影响) ( )
A.正常运转时的输出功率为32 W
B.正常运转时的输出功率为48 W
C.正常运转时的发热功率为1 W
D.正常运转时的发热功率为47W
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com