
4、分组问题:要注意区分是平均分组还是非平均分组,平均分成n组问题别忘除以n!。如4名医生和6名护士组成一个医疗小组,若把他们分配到4所学校去为学生体检,每所学校需要一名医生和至少一名护士的不同选派方法有_______种(答:37440);
3.解排列组合问题的方法有:
(1)特殊元素、特殊位置优先法(元素优先法:先考虑有限制条件的元素的要求,再考虑其他元素;位置优先法:先考虑有限制条件的位置的要求,再考虑其他位置)。如(1)某单位准备用不同花色的装饰石材分别装饰办公楼中的办公室、走廊、大厅的地面及楼的外墙,现有编号为1到6的6种不同花色的石材可选择,其中1号石材有微量的放射性,不可用于办公室内,则不同的装饰效果有_____种(答:300);(2)某银行储蓄卡的密码是一个4位数码,某人采用千位、百位上的数字之积作为十位个位上的数字(如2816)的方法设计密码,当积为一位数时,十位上数字选0. 千位、百位上都能取0. 这样设计出来的密码共有_______种(答:100);(3)用0,1,2,3,4,5这六个数字,可以组成无重复数字的四位偶数_______个(答:156);(4)某班上午要上语、数、外和体育4门课,如体育不排在第一、四节;语文不排在第一、二节,则不同排课方案种数为_____(答:6);(5)四个不同的小球全部放入编号为1、2、3、4的四个盒中。①恰有两个空盒的放法有__________种;②甲球只能放入第2或3号盒,而乙球不能放入第4号盒的不同放法有_________种(答:84;96);(6)设有编号为1、2、3、4、5的五个茶杯和编号为1、2、3、4、5的5个杯盖,将五个杯盖盖在五个茶杯上,至少有两个杯盖和茶杯的编号相同的盖法有_________种(答:31)
(2)间接法(对有限制条件的问题,先从总体考虑,再把不符合条件的所有情况去掉))。如在平面直角坐标系中,由六个点(0,0),(1,2),(2,4),(6,3),(-1,-2),(-2,-1)可以确定三角形的个数为_____(答:15)。
(3)相邻问题捆绑法(把相邻的若干个特殊元素“捆绑”为一个大元素,然后再与其余“普通元素”全排列,最后再“松绑”,将特殊元素在这些位置上全排列)。如(1)把4名男生和4名女生排成一排,女生要排在一起,不同的排法种数为_____(答:2880);(2)某人射击8枪,命中4枪,4枪命中中恰好有3枪连在一起的情况的不同种数为_____(答:20);(3)把一同排6张座位编号为1,2,3,4,5,6的电影票全部分给4个人,每人至少分1张,至多分2张,且这两张票具有连续的编号,那么不同的分法种数是_____(答:144)
(4)不相邻(相间)问题插空法(某些元素不能相邻或某些元素要在某特殊位置时可采用插空法,即先安排好没有限制元条件的元素,然后再把有限制条件的元素按要求插入排好的元素之间)。如(1)3人坐在一排八个座位上,若每人的左右两边都有空位,则不同的坐法种数有_______种(答:24);(2)某班新年联欢晚会原定的5个节目已排成节目单,开演前又增加了两个新节目。如果将这两个节目插入原节目单中,那么不同的插法种数为_____(答:42)。
(5)多排问题单排法。如若2n个学生排成一排的排法数为x,这2 n个学生排成前后两排,每排各n个学生的排法数为y,则x,y的大小关系为_____(答:相等);
(6)多元问题分类法。如(1)某化工厂实验生产中需依次投入2种化工原料,现有5种原料可用,但甲、乙两种原料不能同时使用,且依次投料时,若使用甲原料,则甲必须先投放. 那么不同的实验方案共有_______种(答:15);(2)某公司新招聘进8名员工,平均分给下属的甲、乙两个部门.其中两名英语翻译人员不能同给一个部门;另三名电脑编程人员也不能同给一个部门,则不同的分配方案有______种(答:36);(3)9名翻译中,6个懂英语,4个懂日语,从中选拨5人参加外事活动,要求其中3人担任英语翻译,选拨的方法有____________种(答:90);
(7)有序问题组合法。如(1)书架上有3本不同的书,如果保持这些书的相对顺序不便,再放上2本不同的书,有 种不同的放法(答:20);(2)百米决赛有6名运动A、B、C、D、E、F参赛,每个运动员的速度都不同,则运动员A比运动员F先到终点的比赛结果共有_____种(答:360);(3)学号为1,2,3,4的四名学生的考试成绩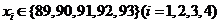 且满足
且满足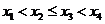 ,则这四位同学考试成绩的所有可能情况有_____种(答:15);(4)设集合
,则这四位同学考试成绩的所有可能情况有_____种(答:15);(4)设集合 ,对任意
,对任意 ,有
,有 ,则映射
,则映射 的个数是_____(答:
的个数是_____(答: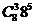 );(5)如果一个三位正整数形如“
);(5)如果一个三位正整数形如“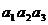 ”满足
”满足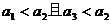 ,则称这样的三位数为凸数(如120、363、374等),那么所有凸数个数为_____(答:240);(6)离心率等于
,则称这样的三位数为凸数(如120、363、374等),那么所有凸数个数为_____(答:240);(6)离心率等于 (其中
(其中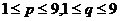 且
且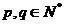 )的不同形状的的双曲线的个数为_____(答:26)。
)的不同形状的的双曲线的个数为_____(答:26)。
(8)选取问题先选后排法。如某种产品有4只次品和6只正品,每只产品均不相同且可区分,今每次取出一只测试,直到4只次品全测出为止,则最后一只次品恰好在第五次测试时,被发现的不同情况种数是_____(答:576)。
(9)至多至少问题间接法。如从7名男同学和5名女同学中选出5人,至少有2名女同学当选的选法有_______种(答:596)
(10)相同元素分组可采用隔板法。如(1)10个相同的球各分给3个人,每人至少一个,有多少种分发?每人至少两个呢?(答:36;15);(2)某运输公司有7个车队,每个车队的车都多于4辆且型号相同,要从这7个车队中抽出10辆车组成一运输车队,每个车队至少抽1辆车,则不同的抽法有多少种?(答:84)
2. 解排列组合问题的依据是:分类相加(每类方法都能独立地完成这件事,它是相互独立的,一次的且每次得出的是最后的结果,只需一种方法就能完成这件事),分步相乘(一步得出的结果都不是最后的结果,任何一步都不能独立地完成这件事,只有各个步骤都完成了,才能完成这件事,各步是关联的),有序排列,无序组合.如(1)将5封信投入3个邮筒,不同的投法共有 种(答:
解排列组合问题的依据是:分类相加(每类方法都能独立地完成这件事,它是相互独立的,一次的且每次得出的是最后的结果,只需一种方法就能完成这件事),分步相乘(一步得出的结果都不是最后的结果,任何一步都不能独立地完成这件事,只有各个步骤都完成了,才能完成这件事,各步是关联的),有序排列,无序组合.如(1)将5封信投入3个邮筒,不同的投法共有 种(答: );(2)从4台甲型和5台乙型电视机中任意取出3台,其中至少要甲型与乙型电视机各一台,则不同的取法共有 种(答:70);(3)从集合
);(2)从4台甲型和5台乙型电视机中任意取出3台,其中至少要甲型与乙型电视机各一台,则不同的取法共有 种(答:70);(3)从集合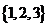 和
和 中各取一个元素作为点的坐标,则在直角坐标系中能确定不同点的个数是___(答:23);(4)72的正约数(包括1和72)共有 个(答:12);(5)
中各取一个元素作为点的坐标,则在直角坐标系中能确定不同点的个数是___(答:23);(4)72的正约数(包括1和72)共有 个(答:12);(5)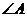 的一边AB上有4个点,另一边AC上有5个点,连同
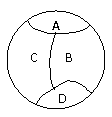
的一边AB上有4个点,另一边AC上有5个点,连同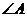 的顶点共10个点,以这些点为顶点,可以构成_____个三角形(答:90);(6)用六种不同颜色把右图中A、B、C、D四块区域分开,允许同一颜色涂不同区域,但相邻区域不能是同一种颜色,则共有 种不同涂法(答:480);(7)同室4人各写1张贺年卡,然后每人从中拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有 种(答:9);(8)
的顶点共10个点,以这些点为顶点,可以构成_____个三角形(答:90);(6)用六种不同颜色把右图中A、B、C、D四块区域分开,允许同一颜色涂不同区域,但相邻区域不能是同一种颜色,则共有 种不同涂法(答:480);(7)同室4人各写1张贺年卡,然后每人从中拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有 种(答:9);(8)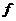 是集合
是集合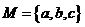 到集合
到集合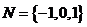 的映射,且
的映射,且
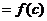 ,则不同的映射共有 个(答:7);(9)满足
,则不同的映射共有 个(答:7);(9)满足 的集合A、B、C共有 组(答:
的集合A、B、C共有 组(答: )
)
1.排列数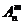 中
中 、组合数
、组合数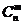 中
中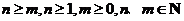 .
.
(1)排列数公式
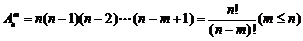 ;
;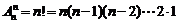 。如(1)1!+2!+3!+…+n!(
。如(1)1!+2!+3!+…+n!(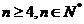 )的个位数字为 (答:3);(2)满足
)的个位数字为 (答:3);(2)满足 的
的 = (答:8)
= (答:8)
(2)组合数公式
 ;规定
;规定 ,
,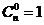 .如已知
.如已知 ,求 n,m的值(答:m=n=2)
,求 n,m的值(答:m=n=2)
(3)排列数、组合数的性质:① ;②
;②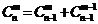 ;③
;③ ;④
;④ ;⑤
;⑤ ;⑥
;⑥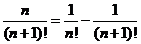 .
.
10.明治维新中最有远见的改革措施是 D
A.改革落后制度,建立新的体制 B.大力改革,发展资本主义经济
C.实行征兵制,建立新式军队 D.大力发展教育,培养建设人才
09.下列哪个选项较适合王安石变法和戊戌变法在教育改革方面的共同点 C
①为改革造舆论并培养人才 ②着眼点在改变中国的社会制度
③改革当时的学校教育制度 ④特别注意培养精通实务的人才
A.①②③ B.②③④ C.①③④ D.①②④
08.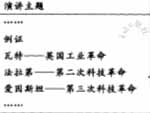 某学者进行了一场学术演讲,演讲提纲如右图所示,你认为该学者演讲的主题是 D
某学者进行了一场学术演讲,演讲提纲如右图所示,你认为该学者演讲的主题是 D
A.重大科学理论的出现是科技革命的先导
B.欧洲是当今世界的科技中心
C.伟大的科技革命造就伟大的科学家
D.伟大的历史人物推动历史进程的大发展
07.“起来,不愿做奴隶的人们,把我们的血肉筑成我们新的长城!”这首创作予1935年,由田汉作词,聂耳谱曲的《义勇军进行曲》后来成为中华人民共和国国歌。《义勇军进行曲》和法国的国歌《马赛曲》的共同之处是 A
①都是在外敌入侵,民族危机的情况下创作的 ②都激发了人民的爱国热情
③都鲜明地体现了革命年代的时代精神 ④都是电影的主题曲
A.①②③ B.①③④ C.②③④ D.①②③④
06.以下图片所示的场景中,不可能出现的现象是 C
 A.对学生述怀:吾十有五而志于学,三十而立,四十而不惑
A.对学生述怀:吾十有五而志于学,三十而立,四十而不惑
B.开创私学之先例,所收学生并无贫富贵贱之分
C.讨论“祸兮福之所倚;福兮祸之所伏。孰知其极?”的问题
D.学生问他何谓“仁”,他说,仁者爱人,己所不欲,勿施于人
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com