
7、设O为坐标原点,M(2,1),点N(x,y)满足 ,则
,则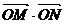 的最大值是( )
的最大值是( )
A、9 B、2 C、12 D、14
6、已知函数y=2sinx的定义域为[a,b],值域为[-2,1],则b-a的值不可能是( )
A、л B、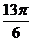 C、
C、 D、
D、
5、已知直线m,n及平面α,下列命题中的真命题是( )
A、若m⊥n,m⊥α,则n∥α B、若m∥n,m⊥α,则n∥α
C、若m⊥α,m⊥α,则m∥n D、若m∥α,n∥α,则m∥n
4、函数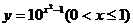 的反函数是( )
的反函数是( )
A、 B、
B、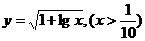
C、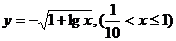 D、
D、
3、在等差数列{an}中前n项和Sn,S5=20,S9=30,则公差d等于( )
A、3
B、-3 C、 D、-
D、-
2、已知向量 不共线,
不共线, 则A、B、C三点共线的充要条件是( )
则A、B、C三点共线的充要条件是( )
A、xy=1 B、x=y=1 C、xy= -1 D、x=y= -1
1、已知集合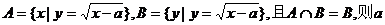 的范围是( )
的范围是( )
A、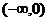 B、
B、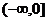 C、
C、 D、
D、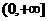
17.(12分)如图所示,ABC为光滑轨道,其中AB段水平放置,BC段是半径为R的圆弧,AB与BC相切于B点。A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧牌原长状态时,物块恰能与固定在墙上的L形挡板相接触于B处但无挤压。现使一质量为m的小球从圆孤轨道上距水平轨道高h处的D点由静止开始下滑,小球与物块相碰后立即共速但不粘连,物块与L形挡板相碰后速度立即减为零也不粘连。(整个过程中,弹簧没有超过弹性限度,不计空气阻力,重力加速度为g)
(1)试求弹簧获得的最大弹性势能。
(2)求小球与物块第一次碰后沿BC上升的最大高h′。
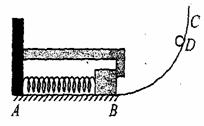 (3)若R>>h,每次从小球接触物块至物块撞击L形挡板历时均为△t,则小球由D点出发经多少时间第三次通过B点?
(3)若R>>h,每次从小球接触物块至物块撞击L形挡板历时均为△t,则小球由D点出发经多少时间第三次通过B点?
16.(12分)如图所示,摩托车做腾跃特技表演,以1.0m/s的初速度沿曲面冲上高0.8m、顶部水平的高台,若摩托车冲上高台的过程中始终以额定功率1.8kW行驶,经过1.2s到达平台顶部,到达顶部后立即关闭发动机油门,人和车落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑。已知圆弧半径为R=1.0m,圆弧所对的圆心角θ=1060,人和车的总质量为180kg,特技表演的全过程中不计一切阻力,取g=10m/s2,sin530=0.8,cos530=0.6。求:(1) 摩托车冲上高台顶部的过程中,摩擦阻力做功不计,则人和车到达顶部平台时的速度v;
(2) A点离平台边缘的水平距离s;
 (3) 人和车运动到圆弧轨道最低点O时对轨道的压力。
(3) 人和车运动到圆弧轨道最低点O时对轨道的压力。
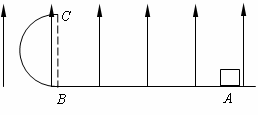
15.(10分)如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小 .求:
.求:
(1)试计算物块在运动过程中克服摩擦力做的功.
(2)证明物块离开轨道落回水平面的水平距离与场强大小E无关,且为一常量.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com