15.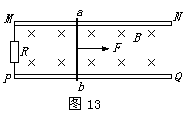(7分)两根平行光滑金属导轨MN和PQ水平放置, 其间距为0.60m, 磁感应强度为0.5OT的匀强磁场垂直轨道平面向下, 两导轨之间连接的电阻R=5.0Ω, 在导轨上有一电阻为 1.0Ω的金属棒ab, 金属棒与导轨垂直, 如图13所示.在ab棒上施加水平拉力F使其以1Om/s的水平速度向右匀速运动.设金属导轨足够长.求:

⑴ 金属棒ab两端的电压.

⑵ 拉力F的大小.

⑶ 电阻R上消耗的电功率.

4.某电池的电动势ε=5V，内电阻r=10Ω，与一个R=90Ω的固定电阻和一个可变电阻R₀串联的电路中，求R₀由零增加到400Ω的过程中，可变电阻R₀上消耗的热功率最大的条件和最大热功率。

　5.一定质量的理想气体，由状态a沿直线变化到状态b，如图21所示。问在此过程中，气体分子的平均速率变化情况如何？

　跟踪训练提示与答案

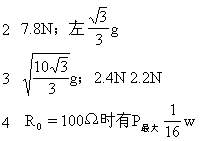
　5 质量一定的理想气体分子的平均速率与其状态参量T相对应，而之积大于4的临界点，即PV乘积最大值，对应的温度最高。因而气体分子的平均速率是先增大后减小的。

3．一个光滑的圆锥面固定在水平桌面上，轴线沿竖直方向，圆锥角θ=60°，如图20。一条长为0.2m的轻质细线，一端固定在圆锥面内的顶点o处，另一端拴着一个质量为0.1kg的物体，悬挂在圆锥面内作水平匀速圆周运动。求：(1)当物体的角速度多大时，物体和圆锥面内表体的拉力多大？物体对圆锥内表面的压力多大？

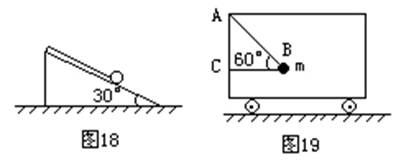
2.如图19所示，小车中有一夹角为60°的轻支架，其右端B处固定一个质量为1kg的重球。求： 　(1)当车以2m/s²的加速度向右匀加速前进时，水平杆BC受到的作用力。

　(2)要使BC杆受力为零，则车的加速度大小和方向又应如何？

1．如图18所示，将质量为1kg的小球挂在倾角为30°的光滑斜面向向右作匀加速运动时，绳对球的拉力和球对斜面的压力。(2)斜面体的加速度至少多大，向哪个方向时，小球对斜面的压力为零？(3)斜面体的加速度至少为多大，向哪个方向时，绳子的张力为零？

6.临界值问题不仅在力学

　临界值问题在电学、热学、光学及综合物理题中是屡见不鲜的，只要抓住出现两种不同物理现象或状态的界，找准制约参量的临界值，这类问题就可迎刃而解，

　[例8]物体在透镜前垂直于透镜主轴放置，通过透镜成放大三倍的像。然后将物体向着透镜平行移近2cm，又得到放大二倍的像。求透镜的焦距。

　[解析]由通过透镜成放大的像，可推知此透镜一定是凸透镜。物体通过凸透镜既可在异侧成放大的实像，又可在同侧成放大的虚像。是放大实像还是放大虚像，是由物距的大小决定的，物距等于焦距是成实像或虚像的临界。所以此题有两解。

　第一种情况：物体从大于焦距处移到小于焦距处，即先成放大实像，后成放大虚像。设透镜焦距为f，先后的物距和像距分别为u₁、u₂、v₁、v₂，由透镜成像公式得

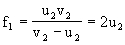
　(v₁=3u₁，｜v₂｜=2u₂)

　由题意u₁-u₂=2(cm)得f₁=2.4(cm)。

　第二种情况：两次物体都在焦点以内，先后都成放大虚像。同理可得

　由题意 u₁-u₂=2(cm)得f₂=12(cm)。

　跟踪训练

5.单向约束解除的可能性(临界值问题)

　如果约束对物体的限制是单侧的，即它只限制物体不得从某一侧脱离约束，但却允许物体从另一侧脱离，在这类约束中，约束反力也是单侧的。对于这种单侧约束，应当注意约束解除的可能性。如在例1中，θ角在0°-90°的范围内是不会解除约束的，当其α角足够大，小球摆动，使θ角＞90°，才可能向内作抛体运动，即约束解除有可能。如θ=180°，而小球仍没有离开圆周，则以后再也不可能离开圆周了。所以约束解除的范围只能在90°＜θ＜180°。如果α角大到可以使小球能以A为圆心，L-r为半径作圆周运动，则小球的单向约束将不能被解除。

　约束解除问题也称临界值问题。在具体问题中，何时解除约束，往往不能预先知道。为了找出约束解除的时刻(或位置)即临界值状态，常用的方法是：先假定物体不脱离约束、将假设的约束反力代入牛顿运动方程中求解，解出约束反力的表达式后，令其约束反力等于零(这就意味着约束解除)，由此可求出相应的时刻(或位置)。

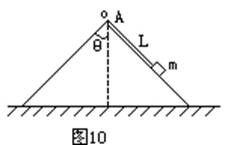
　[例4](83年高考题)一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线之间的夹角为30°(图示10)，一条长度为L的绳(质量不计)一端固定在圆锥体的顶点A处，另一端系着一质量为m的小物体(小物体可看作质点)，物体以速度v绕着圆锥体的轴线作水平匀速圆周运动(物体和绳在附图中都没画出)。求

　运动的，物体不仅受绳的力，而且同时受到锥面的力。受力如图11所示。沿圆周运动的法向和切向建立直角坐标系，

　根据牛顿运动定律的方程得

　Nsin30°+Tcos30°=mg (2)

　解得

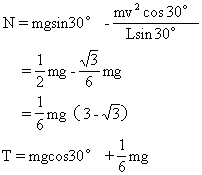
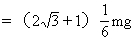
　N为正值说明N的方向与假设相符合。

　(2)当N=0时，斜面对物体的约束解除物体处于临界状态，设此时速度为v₀，

　那么

　Tcos30°=mg(2)

　解得

　面做圆锥摆运动。设绳与竖直夹角为α，受力如图12所示，那么

　解得

　T'=2mg

　α= 45°

　本题中，无论v为何值，绳子的约束是不能解除的。下面两例也是临界问题

　[例5]光滑的斜面上用绳拴一质量为m的小球，如图13所示。当斜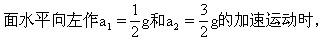求绳上张力分别是多大？

　[解析]当加速度较小时，小球是压在斜面上的，小球受重力G、支持力N和张力T三个力的作用，受力如图14所示。当加速度很大时，小球将飘离斜面，此时小球只受重力G和张力T'的作用，受力如图15所示。为准确判断是属于哪一种情况，必须以小球压在斜面上还是飘离斜面为界，求出其制约参量加速度的临界值a₀。当a＜a₀时，小球压在斜面上，且有支持力存在。当a＞a₀时，小球飘离斜面，当然也就没有支持力存在了。因此解这类问题时，可以先求出临界加速度

　小球将要飘离斜面时，N=0，但绳子与斜面仍然平行。受力如图15所示，其运动方程为

　Tcos45°=ma₀ (1)

　Tsin45°=mg (2)

　联立式(1)、(2)解出a₀=g

　此时小球受力如图14所示。其运动方程为

　Tsin45°+Ncos45°=mg(4)

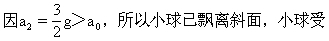　力如图15所示。此时绳与斜面已不再平行，设这时绳与水平方向的夹角为α，其运动方程为

　T′sinα= mg(6)

　[例6]一支圆柱形的玻璃管，质量为20g，密度为2g/cm³，高12cm，容积为20cm³。它的一端封闭，一端开口。现将其开口端竖直向下压入水中，在下压过程中管内的空气不跑出，且温度保持不变。求，当将管口压入水中H₁=4m和H₂=14m深处时，放手后管将如何运动？

　[解析]设管口压入某一深度H₀时，放手后管处于平衡状态。这时管内空气的体积为V₂，管内液面与管口的距离为h₂，与水面的距离为h₁，如图16所示。设玻璃管的体积为V₃，以系统为对象，由平衡条件(忽略管内空气的重力)：

　mg=(V₃+V₂)ρ_水g (1)

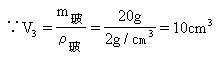
　代入(1)式解得

V₂=10g/cm³

　再以管内封闭的空气为研究对象，取压入水中前为状态1，玻璃管平衡时为状态2，由玻意耳定律有：

P₁V₁=P₂V₂ (2)

∵P₂=P₁+P_水

P_水=P₂-P₁=1×10⁵(Pa)

∴P_水=ρ_水gh₁ h₁=10(m)

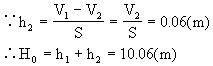
　这是一种不稳定平衡，当压入的深度H₁=4m＜H₀时，浮力大于重力，玻璃管将会变加速上浮；当H₂=14m＞H₀时，浮力小于重力，玻璃管将变加速下沉。H₀是以玻璃管上浮或下沉为界时制约参量水的深度的临界值。

　[例7]如图17所示，一质量为m的小球，带正电荷Q，固定在绝缘细绳oA的B点，oB = r，A端套在以o为圆心，R为半径的光滑圆环上。整个系统同处在光滑绝缘的水平面上，且平面所在的区域具有强度为B方向竖直向上的匀强磁场。当A、B绕o以匀角速ω在水平面上顺时针旋转时，试讨论AB和oB两段绳的张力大小和方向。

　[解析]设当ω=0时，两段绳刚好伸直且张力都为零，而且绳子只能有张力不可能有压力。小球在作圆周运动时，可能受到任一段绳子的张力，令这个张力为T，规定沿半径指向圆心的为正。小球受到的洛仑兹力F_B= BQv = BQωr，它的方向总是沿半径指向圆心的。T与F_B的合力就是小球作圆周运动的向心力。其运动方程为

T+F_B=mω²r

∴T=mω²r－BQωr

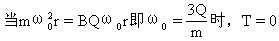
　当ω＞ω₀时，小球受到oB绳指向o的张力，AB段不受力；当ω＜ω₀时，小球受到AB绳沿半径向外的张力，oB段不受力。可见，以两段绳子哪段受力为界，ω₀是制约参量的临界角速度。

4.有摩擦力的约束中的区间问题

　约束反力在约束(曲线或曲面)的垂直方向(法向)，如果有摩擦存在，它却在约束的切线方向。因此在研究有摩擦的约束问题时，先要根据物体有几个可能的运动方向，确定相应的摩擦力的方向。最常见的情况是存在两种可能的运动方向，故而摩擦力的方向也就有两种可能取向。因此，在运用牛顿运动定律列方程时，也将会出现两组，这就导致某些相关量参数有一变化区间。

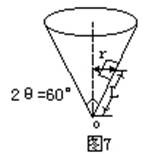　[例3]有一顶角为60°的锥形容器，在距顶点o为L=1.0m处有一质量m=1.0kg的小物体，让物体m与容器一起绕通过o点的竖直轴线作匀速转动(见图7)。(1)若ω₁=5rad/s，则摩擦因数μ至少应为多大才能实现这一情况？(2)若ω₂=8rad/s时，μ应为多大才能实现这一情况？

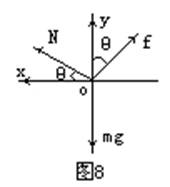　[解析](1)先假设物体有向下滑动的趋势，则摩擦力将沿斜面向上，物体受力如图8所示，沿圆周的切向和法向建立直角坐标系，则牛顿运动定律方程为

　解得

　N＝mgsinθ+mω²Lsinθcosθ

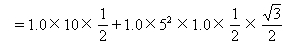
　　=15.8(N)

　f=mgcosθ－mω²Lsin²θ

　 =2.41(N)

　f＞0，说明方向上与假设相符。

　(2)由f=mgcosθ-mω²－mω²Lsin²θ可知

　当f = 0时，w有一个临界角速度ω₀存在。由此得

　mgcosθ=mω²Lsin²θ

　即当ω＜ω₀时，有下滑的趋势，摩擦力向上；当ω＞ω₀时，有上滑趋势，摩擦力向下。ω₂=8rad/s＞ω₀，故f向下，受力如图9所示。牛顿运动定律方程

　Ncosθ+fsinθ=ω₂mLsinθ

　Nsinθ=mg+fcosθ

　解得

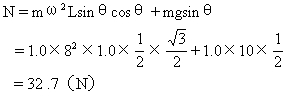
　∴μ₂= f / N=7.34/32.7=0.22

　本题中，如果μ是恒定的，则要使m在确定的高度与锥形容器一起作圆周运动，则角速度ω必有一个变化范围，即当ω＜ω₀时，有下滑趋势，f向上，相应建立牛顿运动方程求出ω的最小值ω_max；当ω＞ω₀时，有上滑趋势，f向下，相应建立牛顿运动方程，求出ω的最大值ω_max，则ω的变化范围是ω_min＜ω＜ω_max。

3．双向约束问题中约束反力的转换

　如果约束从两侧限制物体的运动，则约束反力的方向是可能发生改变的，这一点可以通过下面的例子看出。

　[例2]用细线把质量为M的大圆环挂起来，环上套有两个质量均为m的小环，它们可以在大环上无摩擦地滑动。若两小环同时从大环顶部由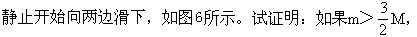则大环会升起来。并求大环开始上升时小环位置θ为多少？

　[解析]此题中小环受到双向约束。设细线张力为T，小环与大环间相互作用力为N(即约束反力)，小球滑到位置θ角时的速度为v。则

　由式(1)、(2)可解得约束反力

　N=mg(3cosθ-2)

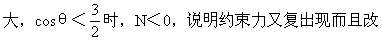　变方向。小环对大环的反作用力将可以提供向上的分力，从而可能使大环升起。

　对大环：T=Mg+2Ncosθ(3)

　当大环升起时，绳子张力T=0，(绳对大环的约束解除)

　∴T=Mg+2Ncosθ

　　 =Mg+2mg(3cosθ-2)cosθ

　　 =0

　6mcos²θ-4mcosθ+M=0

　cosθ有解，此时小环的位置用θ角表示为

2．约束反力的求解

　约束反力的大小及其变化情况，往往不能预先知道，也不是都能由平衡条件计算出来的，而需要根据物体的运动被限制在约束上这一条件，运用牛顿运动定律列方程求解。

　[例1]一质量为m的小球，与长为l的细绳组成一单摆。现将此单摆拉到与竖直线成α角的位置，由静止释放，在摆动途中，摆绳被一钉子A所阻，钉子与摆的悬挂点o相距r，两者连线与竖直线成β角。如图5所示。试求：

　(1)摆绳为钉子所阻后，绳子张力的表达式。

　(2)小球在继续上升的过程中，若摆绳发生弯曲，在此情况下，L、r、β、α之间的关系。

　[解析](1)小球从开始摆动到摆绳发生弯曲之间，都属于单向约束问题。小球摆到图示位置B时，是以钉子A为圆心的，以L-r为半径的圆周运动。设绳子对小球的约束反力为T，AB线与竖直夹角为θ，由机械能守恒定律得

　由牛顿运动定律得此时法向方向方程

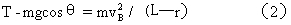
　式(1)、(2)联立解得

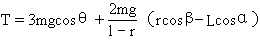
　(2)若绳子发生弯曲，则T=0，意味着约束解除，由此条件求得

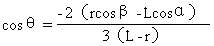
　1＜cosθ＜0

　即　

　由此得出的L，r，α，β应满足的条件为

　3(L-r)＜-2(rcosβ-Lcosα)＜0

　即