
14.(重庆八中2009-2010学年度(上)第二次月考)在数列 中,已知
中,已知 ,
,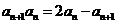 ,
,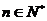 .(1)证明数列
.(1)证明数列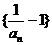 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(2)求证: ,
,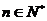 .
.
(1)注意到 ,所以原式整理得:
,所以原式整理得:
由 ,
, 得对
得对 ,
,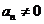 .从而由
.从而由 ,两边取倒数得:
,两边取倒数得: ,即
,即
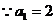 ,
,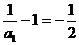
 数列
数列 是首项为
是首项为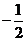 ,公比为
,公比为 的等比数列
的等比数列 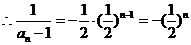
 .
.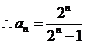 故数列
故数列 的通项公式是
的通项公式是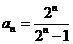 . ……4分
. ……4分
(2)证法1: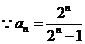 ,
, 当
当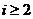 时,
时,

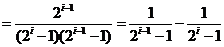 ……8分
……8分
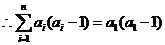
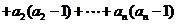
 +
+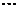
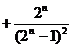


 .…………………………………………………………12分
.…………………………………………………………12分
证法2: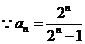 ,
, 当
当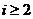 时,
时,
 ………………8分
………………8分

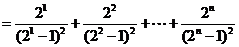
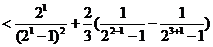

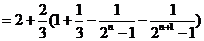
 .………………………………………………………………………………12分
.………………………………………………………………………………12分
13.(余姚中学高三数学期中试卷)
已知函数 ,满足:
,满足:
①对任意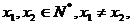 都有
都有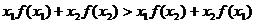 ;②对任意
;②对任意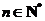 都有
都有 .
.
(1)试证明: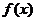 为
为 上的单调增函数;
上的单调增函数;
(2)求 ;
;
(3)令 ,试证明:
,试证明:
解:(1)由①知,对任意 ,都有
,都有 ,
,
由于 ,从而
,从而 ,所以函数
,所以函数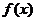 为
为 上的单调增函数.
3分
上的单调增函数.
3分
(2)令 ,则
,则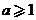 ,显然
,显然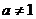 ,否则
,否则 ,与
,与 矛盾.从而
矛盾.从而 ,而由
,而由 ,即得
,即得 .
.
又由(I)知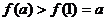 ,即
,即 .
.
于是得 ,又
,又 ,从而
,从而 ,即
,即 .
5分
.
5分
进而由 知,
知,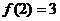 .
.
于是 ,
7分
,
7分
 ,
,
 ,
, ,
,
 ,
, ,
,
由于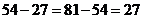 ,
,
而且由(I)知,函数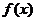 为单调增函数,因此
为单调增函数,因此 .
.
从而 .
9分
.
9分
(3) ,
,
 ,
,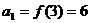 .
.
即数列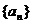 是以6为首项, 以3为公比的等比数列 .
是以6为首项, 以3为公比的等比数列 .
∴  . 11分
. 11分
于是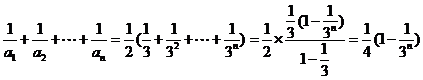 ,
,
显然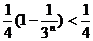 ,
12分
,
12分
另一方面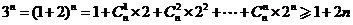 ,
,
从而 .
.
综上所述, 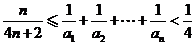 . ---- 15分
. ---- 15分
12.(余杭高级中学2010届高三第四次月考)
已知 ,点
,点 .
.
(Ⅰ)若 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数 的导函数
的导函数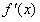 满足:当
满足:当 时,有
时,有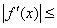
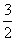 恒成立,求函数
恒成立,求函数
 的解析表达式;
的解析表达式;
(Ⅲ)若 ,函数
,函数 在
在 和
和 处取得极值,且
处取得极值,且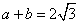 ,证明:
,证明: 与
与 不可能垂直。
不可能垂直。
解:(Ⅰ) 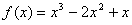 ,
, 
 令
令 得
得 ,解得
,解得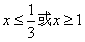
故 的增区间
的增区间 和
和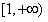 4分
4分
(Ⅱ) (x)=
(x)=
当x ∈[-1,1]时,恒有|
∈[-1,1]时,恒有| (x)|≤
(x)|≤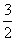 . 5分
. 5分
故有 ≤
≤ (1)≤
(1)≤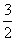 ,
, ≤
≤ (-1)≤
(-1)≤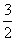 ,
,

11.(台州中学2009-2010学年第一学期期中试题)已知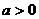 ,函数
,函数 .
.
(1)设曲线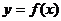 在点
在点 处的切线为
处的切线为 ,若
,若 与圆
与圆 相切,
相切,
求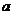 的值;
的值;
(2)求函数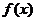 的单调区间; (3)求函数
的单调区间; (3)求函数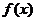 在[0,1]上的最小值。
在[0,1]上的最小值。
解:(1)依题意有 ,
, (1分)
(1分)
过点 的直线斜率为
的直线斜率为 ,所以过
,所以过 点的直线方程为
点的直线方程为 (2分)
(2分)
又已知圆的圆心为 ,半径为1
,半径为1
∴  ,解得
,解得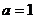 (3分)
(3分)
(2)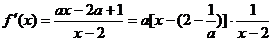
当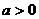 时,
时, (5分)
(5分)
令 ,解得
,解得 ,令
,令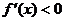 ,解得
,解得
所以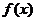 的增区间为
的增区间为 ,减区间是
,减区间是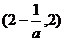 (7分)
(7分)
(3)当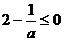 ,即
,即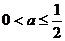 时,
时,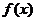 在[0,1]上是减函数
在[0,1]上是减函数
所以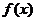 的最小值为
的最小值为 (9分)
(9分)
当 即
即 时
时
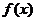 在
在 上是增函数,在
上是增函数,在 是减函数
是减函数
所以需要比较 和
和 两个值的大小(11分)
两个值的大小(11分)
因为 ,所以
,所以
∴ 当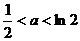 时最小值为
时最小值为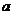 ,当
,当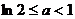 时,最小值为
时,最小值为 (12分)
(12分)
当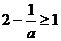 ,即
,即 时,
时,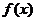 在[0,1]上是增函数
在[0,1]上是增函数
所以最小值为 .
.
综上,当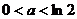 时,
时,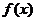 为最小值为
为最小值为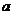
当 时,
时,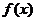 的最小值为
的最小值为 (14分)
(14分)
22.(本小题满分14分)
解:(Ⅰ)

根据已知,
 --------------------4分
--------------------4分

 是
是 公比
公比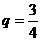 的等比数列。------------------------------6分
的等比数列。------------------------------6分
 ①
①
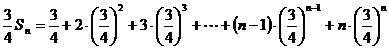 ②
②
①-②得
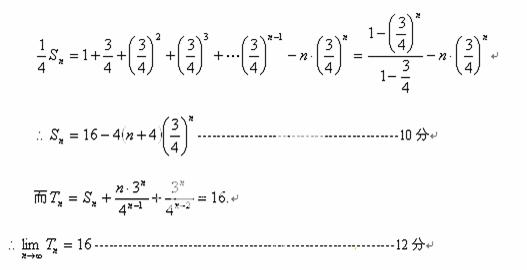
10.(昆一中2010届高三年级第四次月考(12月)
已知 数列
数列 中,对任何正整数
中,对任何正整数 ,等式
,等式 =0都成立,且
=0都成立,且 ,当
,当 时,
时, ;设
;设 .
.
(Ⅰ)求数列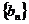 的通项公式;
的通项公式;
(Ⅱ)设 为数列
为数列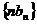 的前n项和,
的前n项和,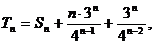 求
求 的值.
的值.
9.(苏皖学校高三第三次月考数学试卷)
已知二次函数f(x)=ax2+bx+c(a,b,c均为实数),满足a-b+c=0,对于任意实数x 都有f (x)-x≥0,并且当x∈(0,2)时,有f (x)≤ .
.
(1)求f (1)的值;
(2)证明:ac≥ ;
;
(3)当x∈[-2,2]且a+c取得最小值时,函数F(x)=f (x)-mx
(m为实数)是单调的,求证:m≤ 或m≥
或m≥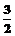 .
.
解:(1)∵对于任意x∈R,都有f (x)-x≥0,且当x∈(0,2)时,
有f
(x) ≤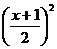 .令x=1
.令x=1
∴1≤f (1) ≤ .
.
即f (1)=1.···················································································· 5分
(2) 由a-b+c=0及f (1)=1.
有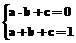 ,可得b=a+c=
,可得b=a+c=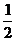 .···················································· 7分
.···················································· 7分
又对任意x,f(x)-x≥0,即ax2-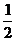 x+c≥0.
x+c≥0.
∴a>0且△≤0.
即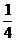 -4ac≤0,解得ac≥
-4ac≤0,解得ac≥ .·························································· 9分
.·························································· 9分
(3) 由(2)可知a>0,c>0.
a+c≥2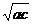 ≥2·
≥2· =
=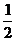 .························································ 10分
.························································ 10分
当且仅当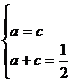 时等号成立.此时
时等号成立.此时
a=c=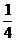 .·······················································································
.·······················································································
∴f
(x)= 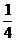 x2+
x2+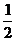 x+
x+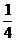 ,
,
F (x)=f (x)-mx=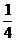 [x2+(2-4m)x+1].····················································· 12分
[x2+(2-4m)x+1].····················································· 12分
当x∈[-2,2]时,f (x)是单调的,所以F (x)的顶点一定在[-2,2]的外边.
∴ ≥2.············································································ 13分
≥2.············································································ 13分
解得m≤-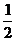 或m≥
或m≥ . …………………………………………………………..14分
. …………………………………………………………..14分
8.(2009-2010学年度淄博市重点高中高三阶段考理科数学)已知数列 的前n项和
的前n项和 (n为正整数)。
(n为正整数)。
(Ⅰ)令 ,求证数列
,求证数列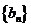 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)令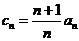 ,
, 比较
比较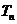 与
与 的大小,并证明。(本小题满分14分)
的大小,并证明。(本小题满分14分)
解:(I)在 中,令n=1,可得
中,令n=1,可得 ,即
,即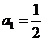
当 时,
时, ,…… 2分
,…… 2分

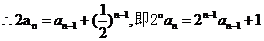 .
.
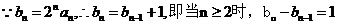 .
.
.
.
又 数列
数列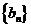 是首项和公差均为1的等差数列. ……………………4分
是首项和公差均为1的等差数列. ……………………4分
于是 .……………………5分
.……………………5分
(II)由(I)得 ,所以
,所以

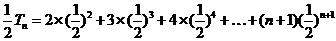
由①-②得
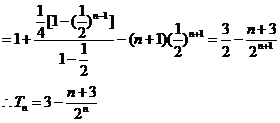
……………………8分

于是确定 的大小关系等价于比较
的大小关系等价于比较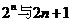 的大小
的大小
由
可猜想当 证明如下:……………………10分
证明如下:……………………10分
证法1:(1)当n=3时,由上验算显示成立。
(2)假设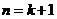 时
时

所以当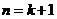 时猜想也成立
时猜想也成立
综合(1)(2)可知
,对一切 的正整数,都有
的正整数,都有
证法2:当 时
时

综上所述,当
 ,当
,当 时
时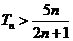
7.(山东省威海市2010届高三上学期教学质量检测)
已知函数 .(Ⅰ)求函数
.(Ⅰ)求函数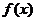 的单调减区间和极值;
的单调减区间和极值;
(Ⅱ)当 时,若
时,若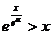 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(Ⅰ)函数 的定义域为
的定义域为 ,
2分
,
2分
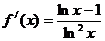 ,令
,令 ,解得
,解得 ,列表
,列表
 |
 |
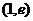 |
 |
 |
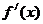 |
- |
- |
0 |
+ |
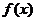 |
单调递减 |
单调递减 |
极小值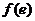 |
单调递增 |
由表得函数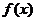 的单调减区间为
的单调减区间为 ,
,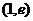 ;极小值为
;极小值为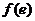 =
= ,无极大值. 6分
,无极大值. 6分
(Ⅱ)因为 ,所以
,所以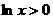
 在
在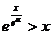 两边取自然对数,
两边取自然对数, ,即
,即 ,
12分
,
12分
由(1)知 的最小值为
的最小值为 ,所以只需
,所以只需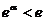 ,即
,即 .
14分
.
14分
6.(山东省临沂高三数学(理工)教学质量监测) 已知函数 (
(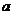 为常数)是R上的奇函数,函数g(x)=
为常数)是R上的奇函数,函数g(x)= 是区间
是区间 上的减函数.
上的减函数.
(Ⅰ)求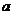 的值;
的值;
(Ⅱ)若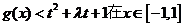 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程 的根的个数.
的根的个数.
解:(Ⅰ)  是奇函数,
是奇函数,
 =
=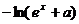 ……1分
……1分
 ,
,
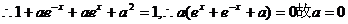 . ……………3分
. ……………3分
(Ⅱ)由(1)知: ,
,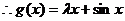 ,
, 上单调递减,
上单调递减,

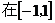 上恒成立,
上恒成立, ……………5分
……………5分
 ,
, 只需
只需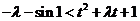 ,
,
 恒成立,
恒成立,
令 =
= ,则
,则 ,
, ,而
,而 恒成立,
恒成立, ……………8分
……………8分
(Ⅲ) 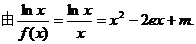 ,
…………………………9分
,
…………………………9分
令
当
 上为增函数;
上为增函数;
当 为减函数;
为减函数;
当 而
而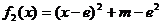 ,……………11分
,……………11分
 方程无解;
方程无解;
 方程有一个根;
方程有一个根;
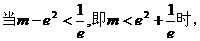 方程有两个根。 …………………………14分
方程有两个根。 …………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com